Abgeschlossene Mengen

Eine Teilmenge $ B $ eines topologischen Raums $ X $ heißt abgeschlossen, wenn es zu jedem Element des Komplements $ u \in X - B $ eine Umgebung gibt, die vollständig in $ X - B $ liegt.
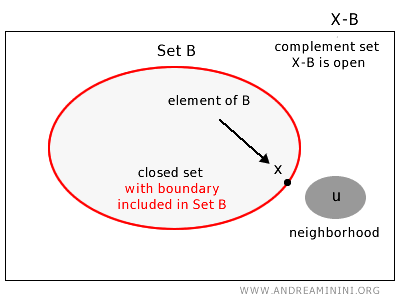
Beispiel einer abgeschlossenen Menge

Mit anderen Worten: Eine Menge ist genau dann abgeschlossen, wenn sie sämtliche ihrer Randpunkte enthält.

Präziser gesagt: Eine Teilmenge $ B $ in einem topologischen Raum $ X $ ist abgeschlossen, wenn ihr Komplement $ X - B $ offen ist.

Hinweis: Daraus folgt, dass es in $ B $ stets Punkte gibt, um die herum sich keine Umgebung finden lässt, die ganz in $ B $ enthalten ist.

Ein anschauliches Beispiel
Das Komplement einer abgeschlossenen Menge
Ein Beispiel
Eigenschaften abgeschlossener Mengen
Beispiel
Weitere Bemerkungen

Ein anschauliches Beispiel

Betrachten wir die reelle Achse $ \mathbb{R} $ und ein abgeschlossenes Intervall.

Was versteht man unter einem abgeschlossenen Intervall? Ein abgeschlossenes Intervall in $ \mathbb{R} $ besteht aus allen Punkten $ x $ mit $ a \leq x \leq b $, wobei $ a $ und $ b $ reelle Zahlen sind, $ a < b $ gilt und beide Endpunkte eingeschlossen werden.

Solche Intervalle schreibt man als $[a,b]$; die eckigen Klammern zeigen an, dass die Endpunkte $ a $ und $ b $ dazugehören.

Zum Beispiel ist $[3,10]$ ein abgeschlossenes Intervall auf der reellen Zahlengeraden $ \mathbb{R} $.

Hier besteht die Menge $ B $ aus allen Zahlen zwischen 3 und 10, einschließlich der Endpunkte.

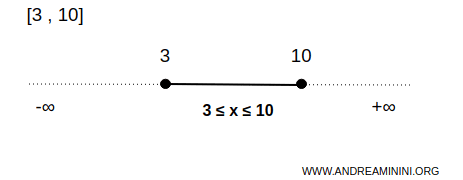
Beispiel eines abgeschlossenen Intervalls

Das heißt: Jeder Punkt $ x $ mit $ 3 \leq x \leq 10 $ liegt in der Menge, also auch $ x=3 $ und $ x=10 $.

Allerdings hat nicht jeder Punkt eine Umgebung, die vollständig in $[3,10]$ enthalten ist.

So enthält jede Umgebung des unteren Endpunkts $ x=3 $ notwendigerweise auch Werte kleiner als 3, die nicht zum Intervall gehören.

Hinweis: Selbst eine winzige Umgebung, etwa $ 3 \pm 0.00000001 $, liegt nicht vollständig in $[3,10]$, da $ 3 - 0.00000001 < 3 $. Dasselbe gilt für den oberen Endpunkt $ x=10 $.

Dies ist ein elementares Beispiel für eine abgeschlossene Menge in einer Dimension.

Weitere Beispiele

Die Idee lässt sich leicht auf die Ebene ($\mathbb{R}^2$) übertragen.

Betrachten wir etwa die Menge aller Punkte in einer Kreisscheibe mit Radius $ r=1 $ und Mittelpunkt im Ursprung $(0,0)$:

$$ x^2 + y^2 \leq 1 $$

Diese Ungleichung beschreibt alle Punkte, deren Abstand vom Mittelpunkt kleiner oder gleich 1 ist - also das Innere der Scheibe zusammen mit dem Randkreis.

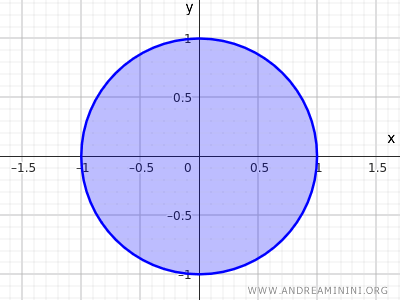
Beispiel einer abgeschlossenen Menge in der Ebene

Auch dies ist eine abgeschlossene Menge.

Man erkennt sofort: Punkte auf dem Randkreis $ x^2 + y^2 = 1 $ besitzen keine Umgebung, die vollständig innerhalb der Kreisscheibe liegt.

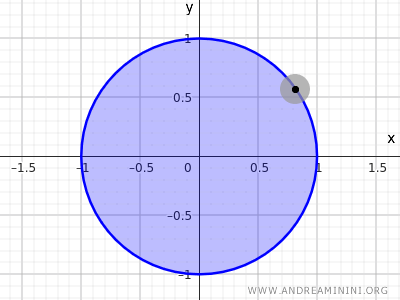
Beispiel einer abgeschlossenen Menge

Hinweis: In der Topologie gilt der Kreis $ x^2 + y^2 = 1 $ im euklidischen Raum $ \mathbb{R}^2 $ weder als offen noch als abgeschlossen, da er nur den Rand, nicht aber das Innere enthält. Die Menge $ x^2 + y^2 \leq 1 $ hingegen ist abgeschlossen, weil sie sowohl das Innere als auch den Rand umfasst und damit alle Randpunkte enthält.

Nach demselben Prinzip lässt sich der Begriff der Abgeschlossenheit auf den dreidimensionalen Raum (Kugel) und allgemein auf den $ n $-dimensionalen Raum (abgeschlossene $ n $-Sphäre) übertragen.

Das Komplement einer abgeschlossenen Menge

In einem topologischen Raum $ X $ ist das Komplement einer abgeschlossenen Menge $ C $ stets eine offene Menge, bezeichnet als $ X - C $.

Mit anderen Worten: Ist $ C $ in $ X $ abgeschlossen, so ist $ X - C $ notwendigerweise offen.

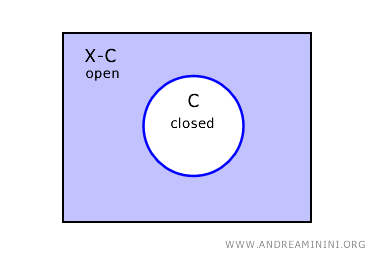
Das Komplement einer abgeschlossenen Menge

Umgekehrt: Ist eine Menge $ U $ offen, dann ist ihr Komplement $ X - U $ abgeschlossen.

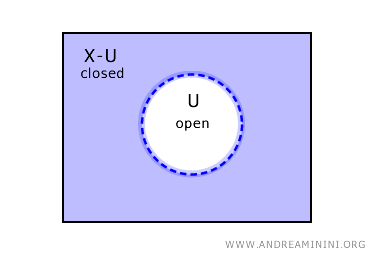
Das Komplement einer offenen Menge

Das sind jedoch nicht die einzigen Möglichkeiten. In manchen topologischen Räumen gibt es Mengen, die gleichzeitig offen und abgeschlossen sind, sowie Mengen, die weder offen noch abgeschlossen sind.

Mit anderen Worten: Nicht abgeschlossen zu sein heißt nicht automatisch offen zu sein - und umgekehrt gilt dasselbe.

Ein Beispiel

Betrachten wir den topologischen Raum $ (X, T) $, wobei $ X = \{a,b,c,d\} $ aus vier Elementen besteht und die Topologie $ T $ durch folgende offene Mengen gegeben ist:

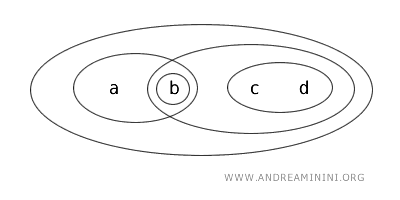
Ein praktisches Beispiel

Die offenen Mengen in dieser Topologie sind: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ sowie die leere Menge $ \varnothing $.

Sehen wir uns einige Fälle an:

$ \{b\} $ ist offen, da sie in der Topologie explizit als offen definiert ist.
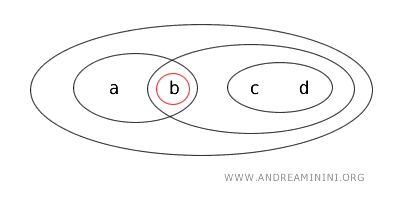
$ \{a\} $ ist abgeschlossen, weil ihr Komplement offen ist. Tatsächlich gilt: $ X - \{a\} = \{b,c,d\} $ ist offen.
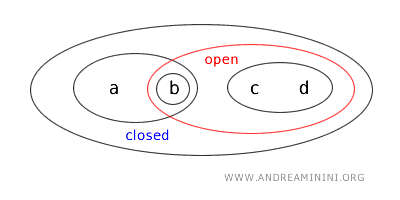
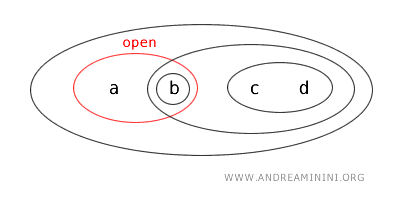
$ \{a,b\} $ ist sowohl offen als auch abgeschlossen (clopen). Während das in den üblichen Topologien auf $ \mathbb{R} $ selten vorkommt, ist es in allgemeineren Räumen durchaus möglich: Eine Menge kann offen und zugleich abgeschlossen sein, wenn auch ihr Komplement offen ist. Hier ist $ \{a,b\} $ per Definition offen, und ihr Komplement $ X - \{a,b\} = \{c,d\} $ ist ebenfalls offen - also ist die Menge auch abgeschlossen.
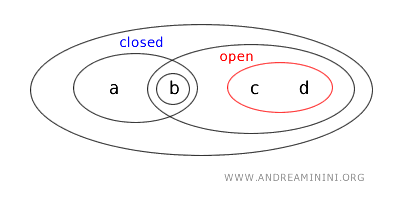
$ \{b,c\} $ ist weder offen noch abgeschlossen. Sie taucht nicht in der Liste der offenen Mengen auf, und ihr Komplement $ X - \{b,c\} = \{a,d\} $ ist ebenfalls nicht offen. Damit erfüllt sie keines der beiden Kriterien.

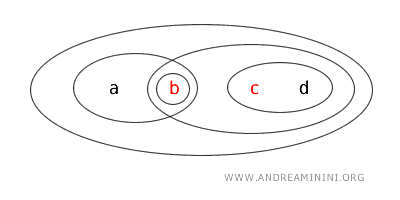
Dieses Beispiel zeigt: In einem topologischen Raum kann eine Menge offen, abgeschlossen, beides zugleich (clopen) oder keines von beiden sein.

Eigenschaften abgeschlossener Mengen

Eine abgeschlossene Menge ist definiert als das Komplement einer offenen Menge. Zu ihren grundlegenden Eigenschaften gehören:

Die leere Menge ($\varnothing$) und der gesamte Raum $ X $ sind immer abgeschlossen.
Der Schnitt beliebig vieler (endlicher wie unendlicher) abgeschlossener Mengen ist wiederum abgeschlossen.
Die Vereinigung endlich vieler abgeschlossener Mengen ist ebenfalls abgeschlossen.

Beispiel

In der Standardtopologie des euklidischen Raums $ \mathbb{R}^n $ ist jeder einzelne Punkt eine abgeschlossene Menge.

Betrachten wir einen Punkt $ n $ auf der reellen Achse ($ \mathbb{R}^1 $). Sein Komplement besteht aus allen Punkten von $ \mathbb{R}^1 $, mit Ausnahme von $ n $.

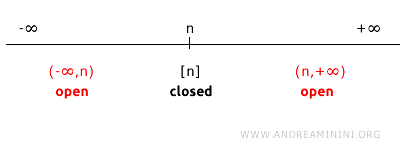
Beispiel

Das Komplement von $\{n\}$ lässt sich als Vereinigung zweier offener Intervalle schreiben: $(-\infty, n) \cup (n, +\infty)$.

Da sowohl $(-\infty, n)$ als auch $(n, +\infty)$ in der Standardtopologie offen sind, ist auch ihre Vereinigung $(-\infty, n) \cup (n, +\infty)$ offen.

Folglich ist $\{n\}$ abgeschlossen, da ihr Komplement offen ist.

Doch in anderen Topologien sind einzelne Punkte nicht notwendigerweise abgeschlossen. Dies hängt von der gewählten topologischen Struktur ab.

Betrachten wir beispielsweise eine Topologie auf $ \mathbb{R} $, die durch die offenen Intervalle $ (n, n+1) $ für jede ganze Zahl $ n $ erzeugt wird. In dieser Topologie sind einzelne Punkte $ n $ keine abgeschlossenen Mengen, da sie sich nicht als Komplement einer offenen Menge darstellen lassen.

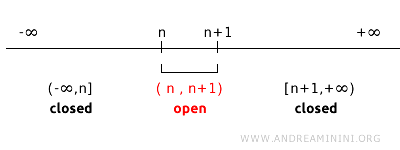
So sind etwa $ (1,2) $ und $ (2,3) $ offene Mengen. Das Komplement von $ (1,2) $ ist $ (-\infty, 1] \cup [2, +\infty) $, während das Komplement von $ (2,3) $ $ (-\infty, 2] \cup [3, +\infty) $ ergibt.

Es existiert hier keine offene Menge, deren Komplement genau $\{2\}$ wäre. Allgemein gilt: Das Komplement einer offenen Menge der Form $ (n, n+1) $ ist stets eine Vereinigung abgeschlossener Intervalle $ (-\infty, n] \cup [n+1, +\infty) $. Daher sind die Punkte $ n $ in dieser Topologie nicht abgeschlossen - ein deutlicher Hinweis darauf, dass Abgeschlossenheit stets von der zugrunde liegenden Topologie abhängt.

Weitere Bemerkungen

Einige ergänzende Hinweise:

Abgeschlossene Mengen und Häufungspunkte
Ein Häufungspunkt einer Menge ist ein Punkt, in dessen jeder Umgebung beliebig kleiner Radius immer weitere Punkte der Menge liegen. Eine Menge ist genau dann abgeschlossen, wenn sie alle ihre Häufungspunkte enthält.

Beispiel: Das abgeschlossene Intervall $[0,1]$ enthält alle seine Häufungspunkte.

So gilt etwa für den Punkt $0{,}5$: Jede offene Umgebung um $0{,}5$ enthält unendlich viele weitere Punkte von $[0,1]$, was ihn zu einem Häufungspunkt macht.
Beispiel: 0.5 als Häufungspunkt im Intervall [0,1]

Dasselbe gilt für die Endpunkte: Der Punkt $0$ ist ein Häufungspunkt, da jede seiner Umgebungen Punkte wie $0.1, 0.01, 0.001$ enthält.
Die Endpunkte des Intervalls [0,1] sind Häufungspunkte
Somit sind alle Punkte von $[0,1]$ Häufungspunkte dieser Menge.

Eine Menge $ A $ ist genau dann abgeschlossen, wenn $ A = \overline{A} $
In einem topologischen Raum gilt: Eine Menge $ A $ ist abgeschlossen, wenn sie mit ihrem Abschluss übereinstimmt, d. h. $ A = \overline{A} $. Der Abschluss $ \overline{A} $ umfasst alle Punkte von $ A $ sowie deren Häufungspunkte. Enthält eine Menge also sämtliche ihrer Häufungspunkte, so ist sie per Definition abgeschlossen.

Und so weiter.