Hausdorff-Raum

Ein Hausdorff-Raum ist ein topologischer Raum, in dem sich zwei verschiedene Punkte stets durch disjunkte offene Umgebungen trennen lassen. Dadurch wird gewährleistet, dass jeder Punkt eindeutig von allen anderen unterscheidbar ist.

Anschaulich bedeutet das Folgendes: Für zwei beliebige Punkte $ x $ und $ y $ existieren offene Mengen $ U $ und $ V $, die die Punkte enthalten und keinen gemeinsamen Schnitt besitzen. Es gilt also $ U \cap V = \emptyset $.

Diese Trennungseigenschaft liefert einen formalen Begriff von Separierbarkeit, der gut mit unserer geometrischen Intuition von Nähe und Distanz im euklidischen Raum übereinstimmt.

Hausdorff-Räume sind in Analysis und Geometrie von zentraler Bedeutung, da sie eine saubere Behandlung von Grenzwerten, Folgenkonvergenz und weiteren fundamentalen topologischen Konstruktionen ermöglichen.

Ein wichtiges Resultat lautet: In jedem Hausdorff-Raum sind einelementige Mengen abgeschlossene Mengen.

Denn das Komplement eines einzelnen Punktes, also die Menge aller übrigen Punkte, ist immer offen.

Praktische Beispiele
Bemerkungen

Praktische Beispiele

Beispiel 1

Betrachten wir die Standardtopologie, die üblicherweise als Topologie auf der reellen Achse $\mathbb{R}$ verwendet wird.

Beispiel der reellen Zahlengeraden

In dieser Topologie sind einzelne Punkte keine offenen Mengen.

Erläuterung: In der Standardtopologie muss jede offene Menge um jeden ihrer Punkte ein vollständiges offenes Intervall enthalten. Da es zwischen zwei reellen Zahlen immer unendlich viele weitere Werte gibt, kann eine einelementige Menge $ \{x\} $ diese Forderung nicht erfüllen. Ihr fehlt der notwendige „Spielraum", um als offen zu gelten. Daher sind einzelne Punkte in der Standardtopologie auf $\mathbb{R}$ nicht offen.

Das Komplement eines Punktes $ \mathbb{R} \setminus \{x\} $ ist hingegen eine offene Menge.

Offene Umgebung als Komplement eines Punktes

Daraus folgt unmittelbar, dass jede einelementige Menge $ \{x\} $ abgeschlossen ist, denn ihr Komplement ist offen.

Zudem ist die Standardtopologie auf $\mathbb{R}$ ein Hausdorff-Raum, weil sich zu je zwei verschiedenen Punkten $ a $ und $ b $ stets offene Umgebungen finden lassen, die sie trennen.

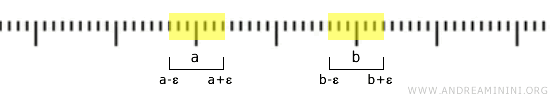
Trennende Umgebungen für a und b

Beispielsweise können wir für $ a < b $ die offenen Intervalle $ (a-\epsilon, a+\epsilon) $ und $ (b-\epsilon, b+\epsilon) $ wählen. Wählt man $ \epsilon $ so klein, dass $ a+\epsilon < b-\epsilon $ gilt, sind die beiden Umgebungen disjunkt.

Damit bestätigt die Abgeschlossenheit einzelner Punkte den Hausdorff-Charakter der Standardtopologie auf $\mathbb{R}$.

Beispiel 2

Betrachten wir nun einen topologischen Raum über der Menge $ X = \{1,2,3\} $, ausgestattet mit der diskreten Topologie.

In der diskreten Topologie ist jeder Punkt per Definition eine offene Menge.

Daraus folgt, dass sämtliche Teilmengen von $ X $ offen sind:

die leere Menge $ \emptyset $
die einelementigen Mengen $ \{1\} $, $ \{2\} $, $ \{3\} $
zweielementige Mengen wie $ \{1, 2\} $, $ \{1, 3\} $, $ \{2, 3\} $
die gesamte Menge $ \{1, 2, 3\} $

Somit gibt es insgesamt $ 2^3 = 8 $ offene Mengen.

Unter dieser Topologie ist der Raum stets ein Hausdorff-Raum.

Nach Definition ist ein Raum Hausdorff, wenn es zu zwei verschiedenen Punkten $ x $ und $ y $ offene Umgebungen $ U $ und $ V $ gibt, sodass $ U \cap V = \emptyset $ und $ x \in U $, $ y \in V $ gilt.

In der diskreten Topologie ist dies sofort erfüllt, denn jeder Punkt ist bereits eine offene Menge. Für verschiedene Punkte $ x $ und $ y $ in $ X $ setzen wir einfach $ U = \{x\} $ und $ V = \{y\} $.

Da $ \{x\} \cap \{y\} = \emptyset $ gilt, ist die Hausdorff-Bedingung erfüllt.

Wählen wir beispielsweise $ x = \{1\} $ und $ y = \{2\} $, so erhalten wir:

$$ \{1\} \cap \{2\} = \emptyset $$

Dieses Beispiel zeigt, dass Punkte in der diskreten Topologie immer durch offene Mengen getrennt werden können.

Dasselbe gilt für jedes andere Punktepaar in $ X $.

In der diskreten Topologie: Sind einzelne Punkte offen oder abgeschlossen?

Diese Frage wirkt auf den ersten Blick ungewöhnlich. Einerseits müssen einpunktige Mengen $ \{x\} $ in einem Hausdorff-Raum abgeschlossen sein. Andererseits sind sie in der diskreten Topologie per Definition offen. Wie passt das zusammen?

Die Antwort ist einfach: In der Topologie kann eine Menge sowohl offen als auch abgeschlossen sein. Solche Mengen heißen clopen. „Abgeschlossen" ist also nicht notwendigerweise das Gegenteil von „offen".

In der diskreten Topologie ist jede einelementige Menge $ \{x\} $ abgeschlossen, weil ihr Komplement aus allen übrigen Punkten besteht und dieses Komplement offen ist. Da jede Teilmenge offen ist, ist folglich auch jedes Komplement offen.

Ein Beispiel: Für $ X = \{1,2,3\} $ ist $ \{1\} $ per Definition offen. Ihr Komplement $ X \setminus \{1\} = \{2,3\} $ ist ebenfalls offen. In der Topologie gilt allgemein: Das Komplement einer offenen Menge ist abgeschlossen.

Damit sind einzelne Punkte $ \{x\} $ in der diskreten Topologie gleichzeitig offen und abgeschlossen.

Offen
Jeder Punkt ist per Definition eine offene Menge.
Abgeschlossen
Das Komplement $ X \setminus \{x\} $ ist offen und macht damit $ \{x\} $ zu einer abgeschlossenen Menge.

Zusammengefasst: einzelne Punkte $ \{x\} $ sind offen, weil jede Teilmenge offen ist, und abgeschlossen, weil ihre Komplemente offen sind.

Ein wesentlicher Unterschied zur Standardtopologie besteht darin, dass dort nicht jede Teilmenge offen ist, sondern nur solche, die für jeden ihrer Punkte eine passende offene Umgebung enthalten.

Bemerkungen

Wichtige Eigenschaften von Hausdorff-Räumen:

In einem Hausdorff-Raum hat jede konvergente Folge genau einen Grenzwert
Eine Folge in einem Hausdorff-Raum $ X $ kann höchstens zu einem einzigen Punkt konvergieren. Würde sie zu zwei verschiedenen Punkten konvergieren, so müssten deren Umgebungen sich schneiden, was im Widerspruch zur Hausdorff-Eigenschaft steht.

Beweis: Sei $ X $ ein Hausdorff-Raum, zum Beispiel $ X = \mathbb{R} $. Angenommen, eine Folge $ x_1, x_2, x_3, \dots $ konvergiert gleichzeitig zu zwei verschiedenen Punkten $ x $ und $ y $. Nach der Definition der Konvergenz existiert eine natürliche Zahl $ N $, sodass für alle $ n > N $ die Punkte $ x_n $ in einer Umgebung $ A $ von $ x $ liegen.

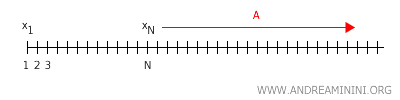
Folge mit Grenzwert x

Gleichzeitig existiert eine natürliche Zahl $ M $, sodass für alle $ n > M $ die Punkte $ x_n $ in einer Umgebung $ B $ von $ y $ liegen.

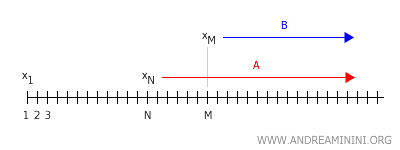
Dieselbe Folge mit Grenzwert y

Gelte $ M > N $, so lägen einige Punkte aus $ A $ zugleich in $ B $. Dann wäre $ A \cap B \neq \emptyset $, was der Hausdorff-Eigenschaft widerspricht. Damit kann eine Folge in einem Hausdorff-Raum nicht zwei verschiedene Grenzwerte haben.