Wegzusammenhängende Räume

Ein topologischer Raum S heißt wegzusammenhängend, wenn sich für jedes Punktpaar A und B in diesem Raum ein stetiger Weg finden lässt, der beide Punkte verbindet, ohne den Raum zu verlassen.

Man stelle sich ein Blatt Papier vor, dessen Ränder nicht berücksichtigt werden.

Dieses Blatt bildet eine durchgehende Fläche und gilt als offen, da die Begrenzung nicht dazugehört.

Für zwei beliebige Punkte A und B auf dem Papier kann man mit einem Stift eine Linie ziehen, ohne ihn dabei abzusetzen.

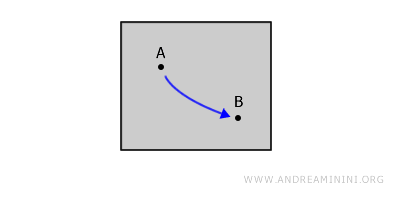
Beispiel für einen wegzusammenhängenden Raum

Mit anderen Worten: Der Weg bleibt vollständig innerhalb des Raumes, in dem die Punkte A und B liegen.

Jeder wegzusammenhängende Raum ist notwendigerweise auch zusammenhängend.

Das wirkt fast selbstverständlich: Wäre ein Raum nicht zusammenhängend, wäre er in getrennte Teile zerlegt, und kein stetiger Weg könnte zwei Punkte miteinander verbinden, ohne den Raum zu verlassen.

Die Umkehrung gilt jedoch nicht in jedem Fall. Nicht jeder zusammenhängende Raum ist zugleich wegzusammenhängend.

Betrachten wir dazu ein Beispiel, das zunächst kontraintuitiv erscheinen mag, aber mathematisch völlig korrekt ist.

Wir definieren zwei Mengen, Q und T:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

Die Menge Q besteht aus allen Punkten der Kurve von sin(1/x), definiert für alle reellen Zahlen R außer null, da dort eine Division durch null vorläge.

Die Menge T enthält lediglich den Punkt null.

Die beiden Mengen Q und T liegen beliebig dicht beieinander, wie der Graph der stetigen Funktion sin(1/x) zeigt.

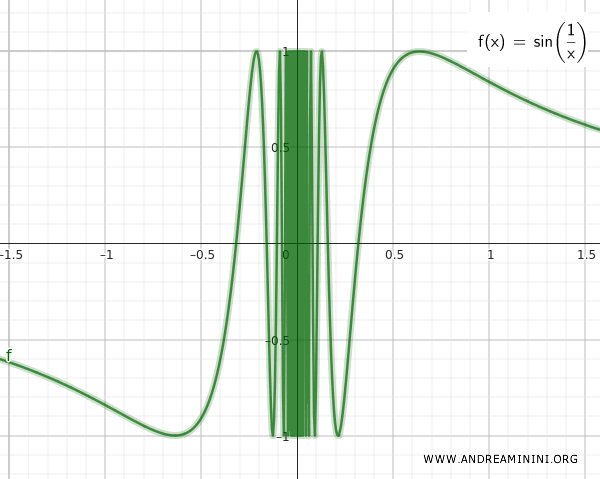
eine Menge, die zusammenhängend, aber nicht wegzusammenhängend ist

Die Vereinigungsmenge S ergibt sich aus Q und T:

$$ S = Q \cup T $$

Die Menge S ist zusammenhängend, da es zu jedem ε>0 eine Umgebung um null (0-ε, 0+ε) gibt, die Punkte aus Q enthält.

Dies gilt, weil null ein Häufungspunkt der Funktion sin(1/x) ist.

Umgebung von null

Dennoch ist S nicht wegzusammenhängend, da es keinen stetigen Weg gibt, der einen Punkt aus Q mit null (aus T) verbindet.

Hinweis: Anders verhält es sich bei der Funktion f(x)=1/x. Hier erkennt man sofort, dass die Mengen Q und T disjunkt sind und keinerlei Häufungspunkt teilen.
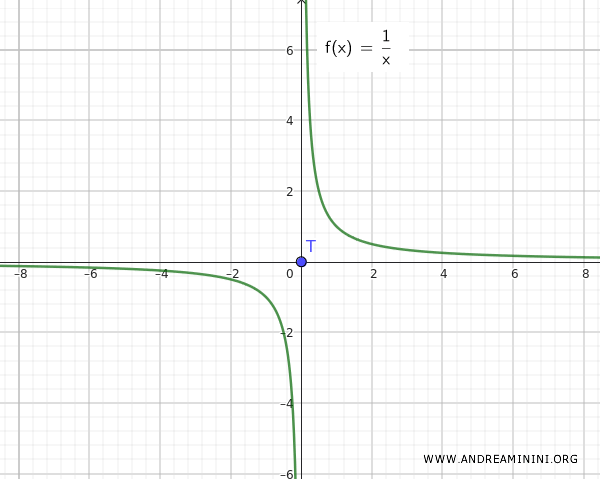
Beispiel für eine nicht zusammenhängende Menge
Dieses Beispiel zeigt, dass die Vereinigung einer zusammenhängenden Menge Q={∀ x ∈ R-{0}, 1/x} mit einem isolierten Punkt T={0} nicht automatisch zusammenhängend ist - es sei denn, der isolierte Punkt (etwa null) ist zugleich ein Häufungspunkt.

Und so weiter.