Zusammenhängende Räume in der Topologie - einfach erklärt

Was bedeutet es, wenn ein Raum zusammenhängend ist?

Anschaulich bedeutet das: Ein Raum ist zusammenhängend, wenn er nicht „auseinanderreißbar“ ist - wenn man ihn also nicht in zwei offene, voneinander isolierte Bereiche aufteilen kann. Gelingt das, dann ist er nicht zusammenhängend, und das Paar $(U,V)$ nennt man eine Trennung.

Hinweis. Dies ist die formale Definition der topologischen Zusammenhängigkeit. Später sehen wir, dass sie nicht immer dasselbe meint wie „durch Wege verbunden“.

Ein einfaches Beispiel

Nehmen wir eine kleine Menge $X$, die aus nur drei Punkten besteht:

$$ X = \{a, b, c\} $$

Je nachdem, wie wir festlegen, welche Teilmengen als „offen“ gelten, erhalten wir unterschiedliche Topologien. Zwei davon sind besonders interessant:

• Topologie A
  $$ \mathcal{T}_A = \{ \emptyset, X, \{a,b\}, \{b\}, \{b,c\} \} $$
• Topologie B
  $$ \mathcal{T}_B = \{ \emptyset, X, \{a,b\}, \{c\}, \{b,c\} \} $$

Welche davon beschreibt einen zusammenhängenden Raum?

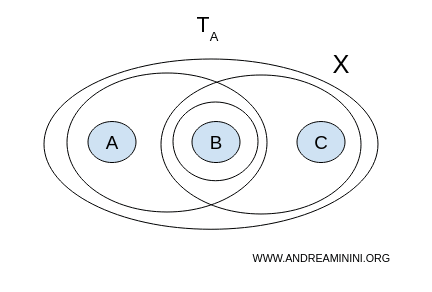
1) Topologie A

Wir prüfen, ob es zwei offene, disjunkte (also nicht überlappende) Mengen gibt, die zusammen ganz $X$ ergeben:

• $U = \{a,b\}, V = \{b,c\}$ → sie überschneiden sich, da beide $b$ enthalten;
• $U = \{a,b\}, V = \{b\}$ → auch hier Überschneidung;
• $U = \{b\}, V = \{b,c\}$ → ebenfalls nicht disjunkt.

Es gibt also keine Möglichkeit, $X$ aufzuteilen, ohne dass sich die Mengen überlappen. Deshalb ist $X$ mit der Topologie A zusammenhängend.

2) Topologie B

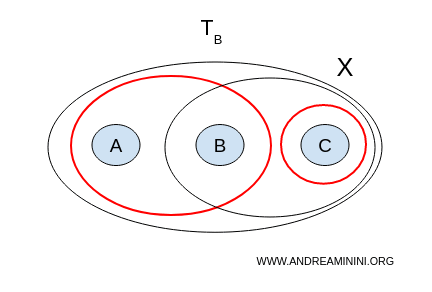
Nun betrachten wir die zweite Topologie:

$$ \mathcal{T}_B = \{ \emptyset, X, \{a,b\}, \{c\}, \{b,c\} \} $$

• $U = \{a,b\}, V = \{b,c\}$ → nicht disjunkt (beide enthalten $b$);
• $U = \{a,b\}, V = \{c\}$ → disjunkt, beide nicht leer, und zusammen ergeben sie $X$.

Hier haben wir also eine echte Trennung. Der Raum $X$ mit der Topologie B ist nicht zusammenhängend.

Merke: Die Zusammenhängigkeit hängt nicht von den Punkten selbst ab, sondern von der gewählten Topologie. Mit denselben Punkten kann eine Topologie den Raum „verbinden“, während eine andere ihn trennt.

Ein klassisches Beispiel: Die reelle Achse ohne einen Punkt

Betrachten wir nun den Raum:

$$ X = (-\infty, n) \cup (n, +\infty) $$

Das entspricht der reellen Achse, bei der der Punkt $n$ entfernt wurde:

$$ X = \mathbb{R} \setminus \{n\} $$

Wir wählen:

$U = (-\infty, n)$ und $V = (n, +\infty)$

• Beide sind offen in der üblichen Topologie der reellen Zahlen.
• Sie sind disjunkt, also ohne gemeinsame Punkte.
• Beide sind nicht leer.

Ihre Vereinigung deckt ganz $X$ ab. Damit erfüllen sie alle Kriterien einer Trennung.

$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$

Folglich ist $X$ nicht zusammenhängend, denn man kann ihn in zwei offene, voneinander isolierte Bereiche teilen.

Hinweis. Wenn man nur einen Punkt von der reellen Achse entfernt, wird ihre Kontinuität unterbrochen. Es bleiben zwei getrennte Regionen - links und rechts vom fehlenden Punkt - , die durch keinen stetigen Weg verbunden werden können. Daher ist dieser Raum nicht nur nicht zusammenhängend, sondern auch nicht wegzusammenhängend.

Topologische Zusammenhängigkeit und Wegzusammenhängigkeit

Diese beiden Begriffe klingen ähnlich, sind aber nicht identisch.

Ein Raum kann topologisch zusammenhängend sein, ohne dass jeder Punkt durch einen stetigen Weg erreichbar ist. Der Unterschied ist subtil, aber wichtig:

• Topologische Zusammenhängigkeit:
  Der Raum lässt sich nicht in zwei offene, disjunkte und nichtleere Teilmengen zerlegen, die zusammen den ganzen Raum bilden.
• Wegzusammenhängigkeit:
  Zwischen jedem Paar von Punkten existiert ein stetiger Weg, der vollständig im Raum verläuft. Ist der Weg zusätzlich injektiv, also ohne Selbstüberschneidung, nennt man den Raum bogenweise zusammenhängend.

Im Allgemeinen gilt: Jeder wegzusammenhängende Raum ist zusammenhängend, aber nicht umgekehrt. Es gibt also zusammenhängende Räume, die keine stetigen Wege zwischen bestimmten Punkten zulassen.

Beispiel: Die berühmte Sinuskurve des Topologen ist ein klassischer Fall:

$$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$

Dieser Raum ist zusammenhängend, da er sich nicht in zwei offene, disjunkte Teilmengen trennen lässt. Trotzdem ist er nicht wegzusammenhängend: Es gibt keinen stetigen Weg, der einen Punkt der schwingenden Kurve mit einem Punkt des vertikalen Segments verbindet.

Das zeigt eindrucksvoll: In der Topologie bedeutet „verbunden“ nicht unbedingt „durch einen Weg erreichbar“. Zusammenhängend zu sein heißt, dass der Raum als Ganzes unteilbar bleibt - selbst dann, wenn keine kontinuierliche Verbindung zwischen allen Punkten existiert.

Anmerkungen

Ergänzende Überlegungen zum Begriff des zusammenhängenden Raums

• Theorem: Charakterisierung zusammenhängender Räume durch offene und abgeschlossene Mengen (clopen)
  Ein topologischer Raum \( X \) heißt zusammenhängend, wenn die einzigen Teilmengen, die gleichzeitig offen und abgeschlossen (clopen) sind, der gesamte Raum \( X \) und die leere Menge \( \emptyset \) sind. Dieses Kriterium bietet eine prägnante und elegante Möglichkeit zu prüfen, ob ein Raum in disjunkte Teilmengen zerlegt werden kann oder ein unteilbares Ganzes bildet.

Weitere Sätze und Beispiele vertiefen dieses Konzept und verdeutlichen, dass der Zusammenhang zu den grundlegenden Strukturprinzipien der Topologie gehört.