Zusammenhängende Räume und clopen-Mengen: Ein grundlegendes Theorem der Topologie

Ein topologischer Raum \( X \) heißt zusammenhängend, genau dann, wenn die einzigen Teilmengen, die sowohl offen als auch abgeschlossen (auch clopen genannt) sind, der gesamte Raum \( X \) und die leere Menge \( \emptyset \) sind.

Mit anderen Worten: Ein Raum ist zusammenhängend, wenn er sich nicht in zwei disjunkte, nichtleere offene Teilmengen zerlegen lässt. In diesem Fall existieren nur zwei clopen-Mengen - der gesamte Raum und die leere Menge.

Dieses Resultat liefert ein grundlegendes Kriterium für den topologischen Zusammenhang. Es ermöglicht, festzustellen, ob ein Raum zusammenhängend ist, ohne auf stärkere Konzepte wie den wegzusammenhängenden Raum (Bogen-Zusammenhang) zurückgreifen zu müssen.

Interpretation

In der Topologie bedeutet das Vorhandensein einer Teilmenge, die gleichzeitig offen und abgeschlossen ist, dass der Raum in zwei offene, disjunkte und nichtleere Teilmengen zerlegt werden kann. Eine solche Zerlegung wird als Trennung des Raums bezeichnet.

Wenn eine Trennung existiert, ist der Raum nicht zusammenhängend. Wenn hingegen die einzigen clopen-Mengen \( X \) und \( \emptyset \) sind, existiert keine Trennung, und der Raum ist zusammenhängend.

Bemerkung: In jedem topologischen Raum sind sowohl der gesamte Raum \( X \) als auch die leere Menge \( \emptyset \) stets zugleich offen und abgeschlossen. Diese beiden trivialen Fälle treten in jeder Topologie auf.

Beispiel 1: Ein endlicher, nicht zusammenhängender Raum

Betrachten wir \( X = \{ a, b, c, d \} \) mit der Topologie \( T \), die durch die offenen Mengen \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \) definiert ist.

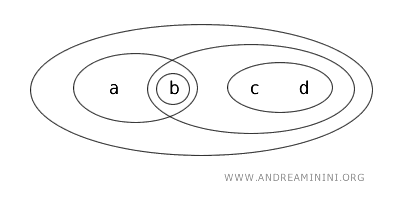
In diesem Fall ist die Teilmenge \( \{ a, b \} \) clopen, weil sie beide Bedingungen erfüllt:

• Sie ist offen, da sie in der Topologie \( T \) enthalten ist.
• Sie ist abgeschlossen, weil ihr Komplement \( X \setminus \{ a, b \} = \{ c, d \} \) ebenfalls offen in \( T \) ist.

Daraus folgt, dass der topologische Raum \( (X, T) \) nicht zusammenhängend ist, da er eine nichttriviale, nichtleere clopen-Menge enthält.

Schon das Vorhandensein einer einzigen nichttrivialen clopen-Menge genügt, um zu zeigen, dass ein Raum nicht zusammenhängend ist. In diesem Beispiel lässt sich der Raum als Vereinigung zweier disjunkter, offener Teilmengen \( \{ a, b \} \) und \( \{ c, d \} \) darstellen, was eine topologische Trennung darstellt und den fehlenden Zusammenhang bestätigt.

Beispiel 2: Die reelle Zahlengerade

Betrachten wir die Menge der reellen Zahlen \( \mathbb{R} \) mit der Standardtopologie, die durch offene Intervalle \( (a, b) \) erzeugt wird.

In dieser Topologie sind Intervalle der Form \( (a, b) \) offen, aber nicht abgeschlossen, während Intervalle der Form \( [a, b] \) abgeschlossen, aber nicht offen sind.

Die einzigen Teilmengen von \( \mathbb{R} \), die sowohl offen als auch abgeschlossen sind, sind \( \mathbb{R} \) selbst und \( \emptyset \). Somit ist die reelle Zahlengerade mit der Standardtopologie ein zusammenhängender topologischer Raum.

Beispiel 3: Ein nicht zusammenhängender Teilraum von \( \mathbb{R} \)

Betrachten wir den Teilraum \( X = (0,1) \cup (2,3) \subset \mathbb{R} \), versehen mit der Teilraumtopologie, die von der Standardtopologie auf \( \mathbb{R} \) induziert wird.

In dieser Topologie sind die Intervalle \( (0,1) \) und \( (2,3) \) sowohl offen als auch abgeschlossen in \( X \), da das Komplement jedes Intervalls im Teilraum \( X \) genau das jeweils andere Intervall bildet. Genauer gilt:

• Das Komplement von \( (0,1) \) in \( X \) ist \( (2,3) \), das offen in \( X \) ist.
• Das Komplement von \( (2,3) \) in \( X \) ist \( (0,1) \), ebenfalls offen in \( X \).

Beide Teilmengen sind also clopen, und der Teilraum \( X \) ist daher nicht zusammenhängend.

Man kann \( X \) als Vereinigung zweier Zusammenhangskomponenten betrachten, nämlich \( (0,1) \) und \( (2,3) \). Diese sind offene, disjunkte und nichtleere Teilmengen. Die Tatsache, dass sich keine stetige Abbildung finden lässt, die einen Punkt der einen Komponente mit einem Punkt der anderen verbindet, charakterisiert den fehlenden Zusammenhang des Raums eindeutig.