Separation einer Teilmenge durch offene Mengen

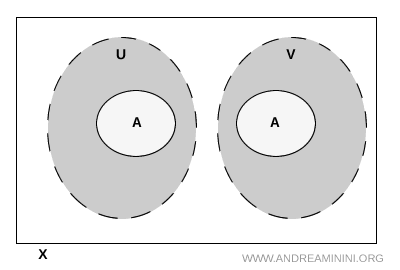
Sei $ A $ eine Teilmenge eines topologischen Raums $ X $. Um zu verstehen, wie sich eine Menge in zwei klar voneinander abgegrenzte Bereiche gliedern lässt, betrachtet man zwei offene Mengen desselben Raums, $ U $ und $ V $. Man sagt, dass sie $ A $ separieren, sobald drei grundlegende Bedingungen erfüllt sind:

Sie überdecken $ A $ vollständig. \[ A \subseteq U \cup V \]
Beide treffen $ A $ nichtleer. \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
Kein Punkt von $ A $ liegt gleichzeitig in beiden offenen Mengen. \[ U \cap V \cap A = \varnothing \]

Wenn diese Voraussetzungen erfüllt sind, zerfällt $ A $ in zwei disjunkte Teilmengen, von denen eine ganz in $ U $ und die andere ganz in $ V $ liegt. Genau dieser klare Schnitt zwischen zwei Bereichen beschreibt die zentrale Idee der Separation in der Topologie.

Der Ansatz über offene Mengen ist eine sehr intuitive Methode, um zu entscheiden, ob eine Teilmenge in einem topologischen Raum tatsächlich getrennt werden kann. Besonders in einführenden Situationen bietet er eine direkte und leicht nachvollziehbare Perspektive.

Grafische Darstellung der Separation einer Teilmenge durch zwei offene Mengen

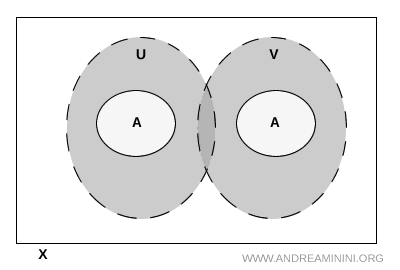
Hinweis. Auch wenn sich $ U $ und $ V $ außerhalb von $ A $ schneiden, ist das für die Separation ohne Bedeutung. Entscheidend ist allein, dass kein Punkt von $ A $ in dieser Schnittmenge liegt. Die relevante Frage lautet also immer: Wie verhalten sich die offenen Mengen relativ zu $ A $?
Grafik, die zeigt, dass eine Schnittmenge zweier offener Mengen außerhalb von A die Separation nicht stört

Ein anschauliches Beispiel

Betrachten wir den Raum $ X = \mathbb{R} $ mit der Standardtopologie. Die betrachtete Menge lautet:

$$ A = [-2,-1] \cup [1,2] $$

Sie besteht aus zwei geschlossenen Intervallen, die klar voneinander getrennt sind.

Nun wählen wir zwei offene Mengen:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Auf der reellen Achse ergibt sich folgendes Bild:

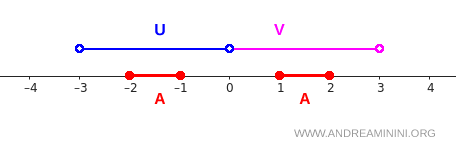
Darstellung der reellen Achse mit den offenen Mengen U und V und den beiden Intervallen von A

Das Intervall $ [-2,-1] $ liegt vollständig in $ U $, das Intervall $ [1,2] $ vollständig in $ V $. Damit lassen sich die drei Bedingungen ohne Mühe überprüfen:

1. $ A $ wird von $ U \cup V $ vollständig überdeckt:

$$ A \subseteq U \cup V $$

2. Beide offenen Mengen treffen $ A $ nichtleer:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

3. Kein Punkt von $ A $ liegt gleichzeitig in beiden offenen Mengen:

$$ U \cap V \cap A = \varnothing $$

Damit steht fest: $ U $ und $ V $ separieren die Teilmenge $ A $ tatsächlich. Gerade weil $ A $ aus zwei voneinander isolierten Stücken besteht, zeigt dieses Beispiel besonders klar, wie die abstrakte Definition in der Praxis funktioniert. Es verdeutlicht, wie offen definierte Strukturen helfen, Trennungen innerhalb eines topologischen Raums sichtbar zu machen.