Homöomorphismen in der Topologie

Ein Homöomorphismus ist in der Topologie eine Abbildung, die bijektiv und stetig ist und deren Umkehrabbildung ebenfalls stetig bleibt.

Im Kern bedeutet das: Man kann einen Raum in einen anderen überführen und auch wieder zurück - ohne dabei etwas zu zerreißen oder anzukleben.

Anders gesagt: Ein Homöomorphismus erlaubt es, einen Raum nahtlos in einen anderen zu verwandeln, ohne dass dabei Teile aufgerissen oder künstlich verbunden werden.

Ein klassisches Beispiel ist die Beziehung zwischen einer Kaffeetasse mit Henkel und einem Donut (Torus) - aus topologischer Sicht sind sie homöomorph. Der Grund: Man kann die Tasse kontinuierlich so verformen, dass sie die Gestalt eines Donuts annimmt, und umgekehrt.

Topologisch betrachtet sind beide Figuren gleichwertig, da sie jeweils genau ein „Loch“ besitzen - beim Donut das zentrale Loch, bei der Tasse die Öffnung des Henkels. Verformt man die Tasse entlang des Henkels, lässt sie sich in die Form eines Donuts überführen.

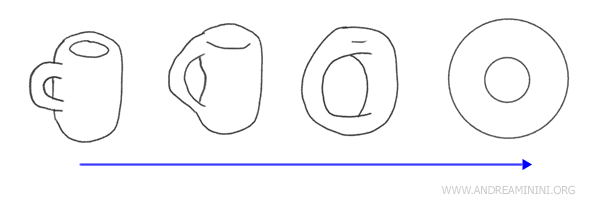
Sind zwei topologische Räume durch einen Homöomorphismus miteinander verbunden, bezeichnet man sie als "homöomorphe Räume". Das heißt: Topologisch sind sie im Wesentlichen identisch, auch wenn sie geometrisch völlig unterschiedlich aussehen können.

Eigenschaften eines Homöomorphismus

Die wesentlichen Merkmale eines Homöomorphismus sind:

• Bijektive Abbildung
  Jedes Element des einen Raumes wird eindeutig einem Element des anderen Raumes zugeordnet - und umgekehrt.
• Stetigkeit
  Ein Homöomorphismus ist notwendigerweise stetig: Kleine Änderungen im Input führen zu kleinen Änderungen im Output.
• Stetige Umkehrabbildung
  Auch die Umkehrfunktion muss stetig sein, sodass die Transformation jederzeit umkehrbar bleibt, ohne die Stetigkeit zu verlieren.
• Erhaltung topologischer Eigenschaften
  Eigenschaften wie Zusammenhang, Kompaktheit und Stetigkeit bleiben erhalten. Die inneren Strukturen des Ausgangsraumes werden also vollständig im Zielraum abgebildet.

Ein Homöomorphismus ist somit eine stetige, umkehrbare Abbildung zwischen zwei topologischen Räumen \(X\) und \(Y\), bei der auch die Umkehrfunktion stetig ist. Dadurch bleiben die topologischen Eigenschaften beider Räume gewahrt.

Kurz gesagt: Ein Homöomorphismus ist eine Möglichkeit, einen Raum in einen anderen „umzuformen“, ohne etwas zu zerreißen oder zusammenzukleben - eine Art „perfekte Entsprechung“ zwischen zwei Strukturen.

Wichtig ist hier die Definition von Stetigkeit in der Topologie:

Seien \(X\) und \(Y\) zwei topologische Räume. Eine Abbildung \(f: X \to Y\) heißt stetig, wenn für jede offene Menge \(V\) in \(Y\) das Urbild \(f^{-1}(V)\) eine offene Menge in \(X\) ist.

Mit anderen Worten: Eine stetige Abbildung in der Topologie „bewahrt“ die Struktur der offenen Mengen, wenn sie Punkte von einem Raum in den anderen überträgt.

Damit ist Stetigkeit in der Topologie eine abstraktere und allgemeinere Fassung des Stetigkeitsbegriffs aus der Analysis.

Hinweis: In der Analysis hängt Stetigkeit vom Begriff des Abstands ab. In der Topologie dagegen basiert sie auf der Struktur offener Mengen - ein Ansatz, der ohne Metrik auskommt.

Ein praktisches Beispiel

Veranschaulichen wir das Konzept des Homöomorphismus und der Stetigkeit nun mithilfe offener Mengen.

Wir betrachten zwei topologische Räume \(X = \{a, b, c, d\}\) und \(Y = \{1, 2\}\).

• Im Raum \(X\) gelten als offen: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• Im Raum \(Y\) gelten als offen: \(\{\}, \{1\}, \{1, 2\}\).

Eine Abbildung \(f: X \rightarrow Y\) ist stetig, wenn für jede offene Menge in \(Y\) das Urbild eine offene Menge in \(X\) ist.

Definieren wir nun \(f: X \rightarrow Y\) folgendermaßen:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Zur Veranschaulichung zeichne ich die Funktion \(f\) und die beiden Räume, wobei die offenen Mengen markiert werden.

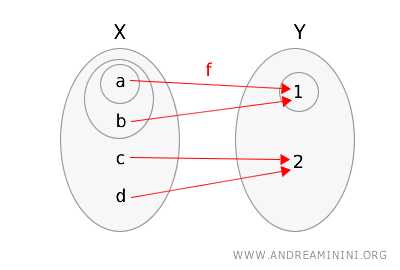
Prüfen wir, ob die Definition erfüllt ist:

• Für die offene Menge \(\{1\}\) in \(Y\) gilt: \(f^{-1}(\{1\}) = \{a, b\}\). Diese Menge ist in \(X\) offen.
• Für die offene Menge \(\{1, 2\}\) in \(Y\) gilt: \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\). Auch diese Menge ist in \(X\) offen.

Da das Urbild jeder offenen Menge in \(Y\) eine offene Menge in \(X\) ist, gilt: Die Funktion \(f\) ist stetig.

Hinweis: Die leere Menge ist definitionsgemäß in jedem topologischen Raum offen und wurde daher nicht eigens überprüft.

Betrachten wir nun eine andere Funktion \(g: X \rightarrow Y\), definiert durch:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Auch hier stellen wir die Funktion \(g\) und die beiden Räume durch Markierung der offenen Mengen dar.

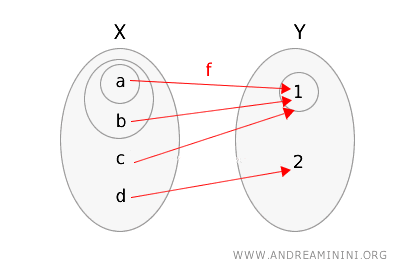
Überprüfen wir die Definition:

• Für die offene Menge \(\{1\}\) in \(Y\) gilt: \(g^{-1}(\{1\}) = \{a, b, c\}\). Diese Menge ist in \(X\) nicht offen.

Da es mindestens eine offene Menge in \(Y\) gibt (hier: \(\{1\}\)), deren Urbild in \(X\) nicht offen ist, folgt: Die Funktion \(g\) ist nicht stetig.

Hinweis: Eine Funktion ist genau dann stetig, wenn für jede offene Menge im Zielraum \(Y\) das Urbild in \(X\) ebenfalls offen ist. Andernfalls ist sie unstetig. Im ersten Beispiel ist \(f\) stetig, weil jedes Urbild offen ist; im zweiten Beispiel ist \(g\) nicht stetig, da dies nicht für alle offenen Mengen gilt.

Definition eines Homöomorphismus

Seien \( X \) und \( Y \) zwei topologische Räume und \( f: X \to Y \) eine bijektive Abbildung mit der Umkehrabbildung \( f^{-1}: Y \to X \). Sind sowohl \( f \) als auch \( f^{-1} \) stetig, so nennt man \( f \) einen Homöomorphismus. In diesem Fall heißen die Räume \( X \) und \( Y \) homöomorph, kurz \( X \cong Y \).

Homöomorphe Räume bezeichnet man auch als topologisch äquivalent.

Was bedeutet das konkret?

Homöomorphie oder topologische Äquivalenz heißt: Zwei Räume sind aus topologischer Sicht „wesentlich gleich“, auch wenn sie geometrisch völlig unterschiedlich aussehen können.

Damit werden die zentralen Eigenschaften eines Homöomorphismus sichtbar:

1. Bijektivität: Die Abbildung \( f: X \to Y \) muss injektiv und surjektiv sein - jedes Element von \( X \) entspricht genau einem Element von \( Y \), und umgekehrt.
2. Stetigkeit von \( f \): Für jede offene Menge in \( Y \) ist das Urbild unter \( f \) eine offene Menge in \( X \).
3. Stetigkeit von \( f^{-1} \): Auch die Umkehrabbildung \( f^{-1}: Y \to X \) muss stetig sein, d. h. das Urbild jeder offenen Menge in \( X \) ist offen in \( Y \).

Beispiel: Man rolle ein Blatt Papier zu einem Zylinder. Zylinder und Blatt sind homöomorph: Man kann den Zylinder ohne Reißen oder Kleben einfach wieder „abrollen“. Die Topologie (die Struktur der offenen Mengen) bleibt unverändert, auch wenn sich die Geometrie ändert.

Wichtig: Die Stetigkeit einer bijektiven Abbildung \( f \) garantiert nicht automatisch, dass auch \( f^{-1} \) stetig ist - das gilt nur, wenn \( f \) zusätzlich eine offene Abbildung ist.

Anders formuliert: Eine bijektive und stetige Abbildung ist nicht zwingend ein Homöomorphismus, solange nicht auch die Umkehrabbildung stetig ist.

Per Definition gilt: Eine Abbildung \( f: X \to Y \) ist stetig, wenn das Urbild jeder offenen Menge in \( Y \) eine offene Menge in \( X \) ist.

Das bedeutet jedoch nicht, dass das Bild jeder offenen Menge in \( X \) ebenfalls offen in \( Y \) sein muss.

Damit auch \( f^{-1} \) stetig ist, muss \( f \) also nicht nur stetig und bijektiv, sondern auch eine offene Abbildung sein.

Beispiel 1

Betrachten wir zwei topologische Räume:

• \( X = (a, b) \) mit \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) mit \( T_Y = \{\emptyset, Y\} \).

Definieren wir \( f: X \to Y \) mit \( f(a) = 1 \), \( f(b) = 2 \).

Die Abbildung \( f \) ist eindeutig bijektiv.

Hinweis: In der Grafik stellen Kreise die offenen Mengen dar. In \( X \) sind \(\{a\}\), \(\{b\}\) und \(X\) offen, in \( Y \) nur \(\{1,2\}\). Leere Mengen sind definitionsgemäß offen, werden hier aber nicht gezeigt.

Prüfen wir die Stetigkeit:

• \( f \) stetig:
  Offene Mengen in \( Y \): \(\emptyset\), \(Y\).
  Urbilder: \( f^{-1}(\emptyset) = \emptyset \) (offen in \( X \)); \( f^{-1}(Y) = X \) (offen in \( X \)).
  ⇒ \( f \) ist stetig.
• \( f^{-1} \) nicht stetig:
  Offene Mengen in \( X \): \(\{a\}\), \(\{b\}\), \(X\).
  Urbilder: \( f^{-1}(\{a\}) = \{1\} \) (nicht offen in \( Y \)), \( f^{-1}(\{b\}) = \{2\} \) (nicht offen in \( Y \)).
  ⇒ \( f^{-1} \) ist nicht stetig.

Fazit: \( f \) ist bijektiv und stetig, aber kein Homöomorphismus, da \( f^{-1} \) nicht stetig ist.

Hinweis: Das Problem liegt in der unterschiedlichen Feinheit der Topologien: \( X \) hat feinere offene Mengen (\(\{a\}, \{b\}\)), \( Y \) dagegen nur \(\{\emptyset, Y\}\).

Beispiel 2

Nun ein anderes Paar von Räumen:

• \( X = (a, b) \) mit \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) mit \( T_Y = \{\emptyset, \{1\}, Y\} \).

Definieren wir \( f: X \to Y \) mit \( f(a) = 1 \), \( f(b) = 2 \).

Auch hier ist \( f \) bijektiv.

Überprüfen wir die Stetigkeit:

• \( f \) stetig:
  Offene Mengen in \( Y \): \(\emptyset\), \(\{1\}\), \(Y\).
  Urbilder: \( f^{-1}(\{1\}) = \{a\} \) (offen in \( X \)), \( f^{-1}(Y) = X \), \( f^{-1}(\emptyset) = \emptyset \).
  ⇒ \( f \) ist stetig.
• \( f^{-1} \) stetig:
  Offene Mengen in \( X \): \(\{a\}\), \(X\).
  Urbilder: \( f^{-1}(\{a\}) = \{1\} \) (offen in \( Y \)), \( f^{-1}(X) = Y \).
  ⇒ \( f^{-1} \) ist stetig.

Hier ist \( f \) sowohl bijektiv und stetig als auch seine Umkehrabbildung stetig. Somit ist \( f \) ein Homöomorphismus.

Hinweis: Dieses Beispiel zeigt: Mit einer geeigneten Wahl der Topologien auf \( X \) und \( Y \) erhält man eine bijektive, stetige Abbildung mit stetiger Umkehr - im Unterschied zum ersten Beispiel.

Homöomorphismen und andere topologische Transformationen

Der Begriff „Homöomorphismus“ wird oft in einem weiteren Sinn im Zusammenhang mit topologischen Transformationen gebraucht, bezeichnet jedoch eine klar definierte Unterklasse dieser Abbildungen.

Topologische Transformationen und Homöomorphismen sind eng verwandt, müssen aber begrifflich unterschieden werden:

• Topologische Transformationen
  Dieser Sammelbegriff umfasst alle Abbildungen, die einen topologischen Raum verändern, ohne grundlegende topologische Eigenschaften wie Zusammenhang oder Stetigkeit zu zerstören. Dazu gehören nicht nur Homöomorphismen, sondern auch Isotopien, Homotopien oder Diffeomorphismen.
• Homöomorphismen
  Ein Homöomorphismus ist der Spezialfall einer bijektiven und stetigen Abbildung mit stetiger Umkehrabbildung. Er erlaubt es, Räume vollständig und reversibel ineinander zu überführen. Zwei homöomorphe Räume gelten aus topologischer Sicht als identisch - selbst wenn sie geometrisch sehr unterschiedlich erscheinen.

Jeder Homöomorphismus ist somit eine topologische Transformation, doch nicht jede topologische Transformation erfüllt die strengen Voraussetzungen, die für Homöomorphismen gefordert sind.

Einige Transformationen besitzen eigene Eigenschaften oder Einschränkungen, die sie von Homöomorphismen abgrenzen.

Weiterführende Anmerkungen

Einige ergänzende Überlegungen zum Begriff des Homöomorphismus:

• Topologische Eigenschaft
  Eine topologische Eigenschaft ist ein Merkmal eines topologischen Raums, das unter Homöomorphismen unverändert bleibt. Sind zwei Räume homöomorph - das heißt, es existiert eine stetige Bijektion mit stetiger Umkehrabbildung - so teilen sie dieselben topologischen Eigenschaften.
• Hausdorffs Theorem über Homöomorphismen
  Dieses Theorem besagt: Ist \( f: X \to Y \) ein Homöomorphismus und \( X \) ein Hausdorff-Raum, dann ist auch \( Y \) notwendigerweise ein Hausdorff-Raum. Da Homöomorphismen topologische Eigenschaften bewahren, wird die Hausdorff-Eigenschaft von \( X \) auf \( Y \) übertragen.
• Das algebraische Analogon zum Homöomorphismus ist der Gruppenisomorphismus: Dort bewahrt die bijektive Abbildung die algebraische Struktur der Gruppenoperation, während beim Homöomorphismus die Struktur der offenen Mengen in topologischen Räumen erhalten bleibt.

Weitere Aspekte lassen sich entsprechend fortführen.