Die Standardtopologie einer offenen Menge

Die Standardtopologie auf $ \mathbb{R} $ beschreibt, wie man „Offenheit“ auf der reellen Zahlengeraden versteht. Grundlage sind die offenen Intervalle $ (a, b) $ mit $ a < b $. Jede Vereinigung solcher Intervalle - ob endlich oder unendlich - gilt ebenfalls als offene Menge.

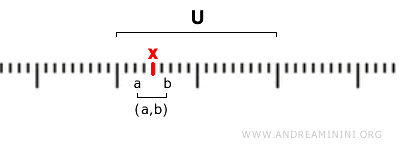
Formuliert man es etwas genauer, so heißt eine Menge $ U $ offen, wenn zu jedem Punkt $ x \in U $ ein offenes Intervall $ (a, b) $ existiert, das $ x $ enthält und vollständig in $ U $ liegt.

$$ x \in (a,b) \subseteq U $$

Mit anderen Worten: Jeder Punkt $ x $ einer offenen Menge $ U $ liegt in einem offenen Intervall, das ganz in $ U $ enthalten ist. Das ist das Grundprinzip der Standardtopologie.

Beispiel einer offenen Menge

In dieser Topologie gelten folgende Mengen als offen:

Offene Intervalle
Die offenen Mengen auf $ \mathbb{R} $ sind genau die Intervalle $ (a, b) $ mit $ a < b $ - und alle möglichen Vereinigungen solcher Intervalle.
Operationen mit offenen Mengen
Die Offenheit bleibt unter bestimmten Operationen erhalten:
- Vereinigungen: Jede - auch unendliche - Vereinigung offener Mengen bleibt offen.
- Endliche Schnitte: Der Schnitt einer endlichen Anzahl offener Mengen ist ebenfalls offen.

Die Standardtopologie ist nur eine von vielen möglichen Topologien auf einer Menge $ X $. Man nennt sie „standard“, weil sie im Alltag der Mathematik die meistverwendete ist - sie bildet das Fundament für Begriffe wie Stetigkeit, Nähe und Grenzwert.

Ihr besonderer Reiz liegt darin, dass sie etwas intuitiv so Alltägliches wie „in der Nähe liegen“ oder „eine Umgebung haben“ präzise in mathematische Sprache übersetzt.

Hinweis: Auf $ \mathbb{R} $ und anderen Räumen kann man auch alternative Basen wählen, die zu ganz anderen offenen Mengen führen. Solche Varianten dienen oft dazu, spezielle Eigenschaften zu untersuchen oder neue Perspektiven auf bekannte Strukturen zu eröffnen.

Ein praktisches Beispiel

Die Basis der Standardtopologie auf $ \mathbb{R} $ besteht aus allen offenen Intervallen $ (a, b) $ mit $ a < b $.

$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$

Für jeden Punkt $ x $ in einer offenen Menge $ U $ lässt sich also stets ein offenes Intervall um $ x $ finden, das vollständig in $ U $ liegt. Das entspricht genau der Definition einer offenen Menge in der Standardtopologie.

$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$

So wird deutlich: $ U $ ist offen in der Standardtopologie auf $ \mathbb{R} $.

Diese Topologie ist die vertrauteste auf der reellen Achse - sie ist die Grundlage, wenn man in der Analysis von „Stetigkeit“ oder „Grenzwert“ spricht.

Beispiel 2

Betrachten wir das Intervall $ (0,1) $, das die Endpunkte $ 0 $ und $ 1 $ ausschließt. Wie sieht seine Struktur in der Standardtopologie aus?

Die Frage ist, ob $ (0,1) $ selbst ein topologischer Raum sein kann - und die Antwort lautet: ja, mit der sogenannten induzierten Topologie.

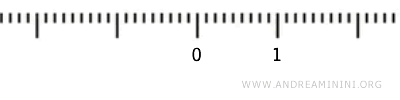
Fall des Intervalls (0,1)

Eine Teilmenge $ U \subset (0,1) $ ist in dieser induzierten Topologie offen, wenn es zu jedem Punkt $ x \in U $ ein Intervall $ (a,b) $ in $ \mathbb{R} $ gibt, das $ x $ enthält und für das $ (a,b) \cap (0,1) \subseteq U $ gilt.

So lässt sich $ (0,1) $ als Schnitt mehrerer offener Mengen der reellen Standardtopologie darstellen - es besitzt also eine klar definierte topologische Struktur.

Das Intervall $ (0,1) $ bildet somit einen eigenen topologischen Raum mit der von $ \mathbb{R} $ abgeleiteten Standardtopologie.

Zum Beispiel sind die Intervalle $ (0.1, 0.5) $, $ (0.2, 0.9) $ oder ihre Vereinigung $ (0.1, 0.5) \cup (0.6, 0.8) $ offene Mengen von $ (0,1) $ in der induzierten Topologie. Das bedeutet: Die offenen Mengen von $ (0,1) $ sind genau jene offenen Mengen von $ \mathbb{R} $, deren Schnitt mit $ (0,1) $ vollständig innerhalb dieses Intervalls liegt.

Da $ (0,1) $ ein Teilraum von $ \mathbb{R} $ ist, erbt es alle grundlegenden Eigenschaften der Standardtopologie.

Beispiel 3

Betrachten wir nun die endliche Menge $ X = \{1,2,3\} $. Kann man ihr eine ähnliche Struktur geben?

Hier funktioniert das Prinzip der offenen Intervalle nicht mehr - die Basis der Standardtopologie passt schlicht nicht zu einer diskreten Menge wie $ X $.

Das Element $ \{2\} $ zum Beispiel liegt zwar in einem offenen Intervall $ (2-\epsilon, 2+\epsilon) $, dieses Intervall enthält jedoch unendlich viele reelle Zahlen, die nicht zu $ X $ gehören. Daher kann $ \{2\} $ nicht als offen in der Standardtopologie auf $ \mathbb{R} $ gelten.
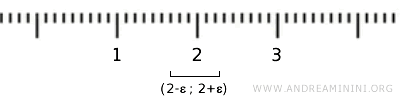
Beispiel mit der Zahl 2

Betrachtet man $ X $ als Teilmenge von $ \mathbb{R} $, enthält die sogenannte „Teilraumtopologie“ nur zwei offene Mengen: die leere Menge und $ X $ selbst - also eine sehr einfache, fast triviale Struktur.

Will man einer endlichen Menge wie $ X $ eine reichere topologische Form geben, wählt man in der Regel die diskrete Topologie. In ihr gilt: Jede Teilmenge ist per Definition offen.

Und das ist der Ausgangspunkt, um die Vielfalt der Topologien wirklich zu entdecken.