Produkttopologie auf topologischen Räumen

Seien $X$ und $Y$ zwei topologische Räume. Die Produkttopologie auf dem kartesischen Produkt $X \times Y$ ist die Topologie, die durch eine Basis $B$ erzeugt wird. Diese Basis besteht aus allen Mengen der Form $U \times V$, wobei $U$ eine offene Teilmenge von $X$ und $V$ eine offene Teilmenge von $Y$ ist. Formal schreibt man: $$ B = \{ U \times V \mid U \text{ ist offen in } X \text{ und } V \text{ ist offen in } Y \} $$

Die Idee hinter der Produkttopologie ist einfach: Man überträgt das Konzept offener Mengen aus den einzelnen Räumen $X$ und $Y$ auf ihr Produkt $X \times Y$, indem man offene Mengen in beiden Räumen kombiniert.

Die so entstehenden Mengen $U \times V$ bilden eine topologische Basis.

Eine topologische Basis ist eine Sammlung offener Mengen, aus der sich jede weitere offene Menge des Raumes durch Vereinigungen zusammensetzen lässt.

Ein zentrales Merkmal der Produkttopologie ist daher: Das kartesische Produkt zweier offener Mengen ist selbst wieder offen.

Bemerkung: Die offenen Mengen der Produkttopologie beschränken sich nicht auf einzelne Produkte $U \times V$. Auch beliebige Vereinigungen solcher Produkte gehören dazu. Die Menge $B$ ist daher keine vollständige Topologie, sondern lediglich eine Basis, aus der alle offenen Mengen erst entstehen.

Ein analoges Verhalten findet man auch bei abgeschlossenen Mengen.

In der Produkttopologie gilt: Das kartesische Produkt zweier abgeschlossener Mengen ist abgeschlossen.

Allerdings lässt sich nicht jede abgeschlossene Menge der Produkttopologie als Produkt abgeschlossener Mengen schreiben.

Wie bei den offenen Mengen entstehen also auch bei den abgeschlossenen Mengen neue Strukturen, die über einfache kartesische Produkte hinausgehen.

Ein anschauliches Beispiel
Produkt mehrerer topologischer Räume
Basis der Produkttopologie
Abschließende Bemerkungen

Ein anschauliches Beispiel

Ein konkretes Beispiel macht den Aufbau der Produkttopologie besonders deutlich.

Wir betrachten die folgenden topologischen Räume:

$X = \mathbb{R}$, die reelle Zahlengerade mit ihrer Standardtopologie, deren offene Mengen durch offene Intervalle $(a, b)$ beschrieben werden.
$Y = \mathbb{R}$, ebenfalls mit der Standardtopologie.

Das Produkt $X \times Y$ ist in diesem Fall die euklidische Ebene $\mathbb{R}^2$.

Die Basis $B$ der Produkttopologie besteht aus allen Mengen $U \times V$, wobei $U$ und $V$ offene Intervalle der reellen Achse sind.

Wählen wir zum Beispiel $U = (1, 2)$ und $V = (3, 4)$.

Dann ist $U \times V = (1, 2) \times (3, 4)$ eine offene Menge in $\mathbb{R}^2$. Geometrisch handelt es sich um ein offenes Rechteck in der Ebene.

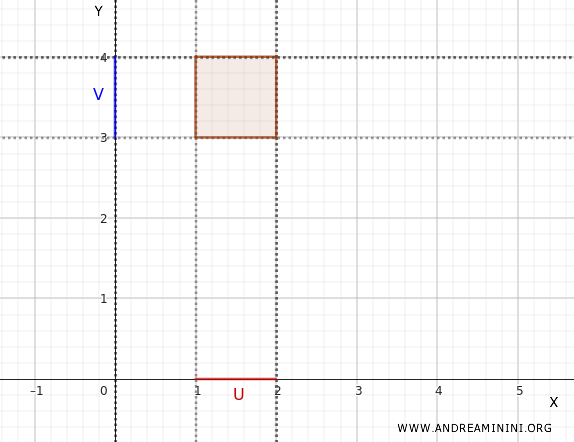
offenes Rechteck als Basisoffenes der Produkttopologie

Interessant wird es, wenn man mehrere solcher Basismengen kombiniert.

Betrachten wir die beiden offenen Rechtecke $ (1, 2) \times (3, 4) $ und $ (1.5, 2.5) \times (3.5, 4.5) $.

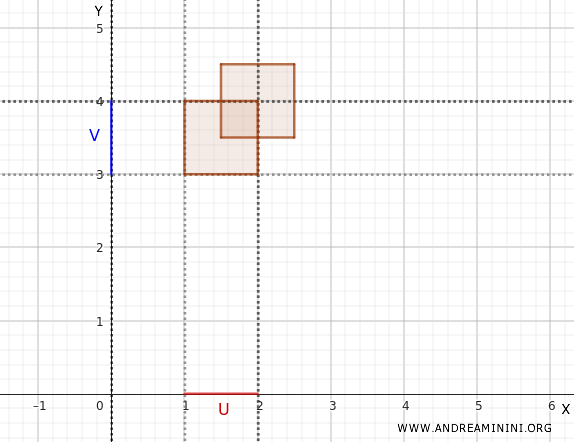
Vereinigung zweier Basisoffener in der Produkttopologie

Die Vereinigung dieser beiden Mengen ist kein einzelnes kartesisches Produkt mehr. Dennoch ist sie offen, da sie als Vereinigung von Basiselementen entsteht:

$$ (1, 2) \times (3, 4) \cup (1.5, 2.5) \times (3.5, 4.5) $$

Das zeigt: Jeder Punkt der Ebene liegt in einer Vereinigung von Mengen der Form $U \times V$.

So gehört etwa der Punkt $(1.8, 3.8)$ zu einem der Rechtecke und damit auch zur Vereinigung.

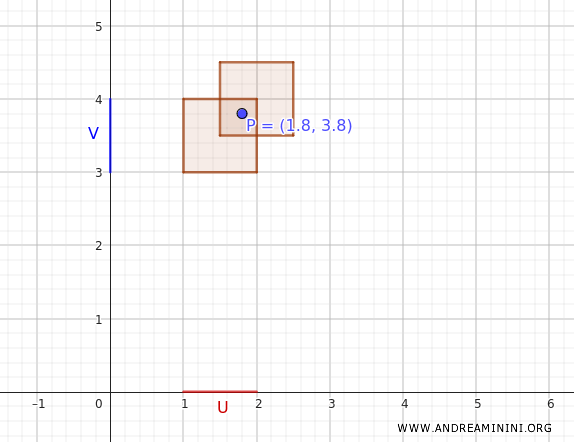
Punkt in einer Vereinigung von Basisoffenen

Dieses Beispiel verdeutlicht, wie die Basis $B$ Schritt für Schritt die gesamte Produkttopologie erzeugt.

Bemerkung: Die Produkttopologie ist besonders wichtig, weil sie es erlaubt, die offenen Strukturen der einzelnen Räume systematisch auf ihren Produktraum zu übertragen.

Beispiel 2

Zum Abschluss betrachten wir ein Beispiel mit endlichen topologischen Räumen.

$X = \{a, b, c\}$ mit der Topologie $\{\emptyset, \{a\}, \{b, c\}, X\}$
$Y = \{1, 2\}$ mit der Topologie $\{\emptyset, \{1\}, Y\}$

Um die Produkttopologie auf $X \times Y$ zu bestimmen, bildet man alle kartesischen Produkte offener Mengen aus $X$ und $Y$ und nimmt anschließend alle möglichen Vereinigungen.

$$ B = \{ U \times V \mid U \text{ ist offen in } X \text{ und } V \text{ ist offen in } Y \} $$

Die offenen Mengen von $X$ sind:

$\emptyset$
$\{a\}$
$\{b, c\}$
$X$

Die offenen Mengen von $Y$ sind:

$\emptyset$
$\{1\}$
$Y$

Daraus ergeben sich unter anderem die folgenden kartesischen Produkte:

$\{a\} \times \{1\} = \{(a, 1)\}$
$\{a\} \times Y = \{(a, 1), (a, 2)\}$
$\{b, c\} \times \{1\} = \{(b, 1), (c, 1)\}$
$\{b, c\} \times Y = \{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Bemerkung: Ist eine der beiden Mengen leer, so ist auch ihr kartesisches Produkt leer, da keine geordneten Paare gebildet werden können.

Die Produkttopologie auf $X \times Y$ besteht aus allen möglichen Vereinigungen dieser Mengen.

Man erkennt auch hier deutlich: Die offenen Mengen der Produkttopologie sind nicht auf einfache Produkte $U \times V$ beschränkt. Auch deren Vereinigungen sind offen.

Beispielsweise ist $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$ eine offene Menge der Produkttopologie.

Die Basis $B$ der Produkttopologie besteht aus den nichtleeren kartesischen Produkten offener Mengen.

$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y$

Produkt mehrerer topologischer Räume

Die Produkttopologie lässt sich ohne zusätzliche Schwierigkeiten auf Produkte von mehr als zwei topologischen Räumen übertragen. Das zugrunde liegende Prinzip bleibt dabei unverändert.

Seien $ n $ topologische Räume $ X_1, X_2, \dots, X_n $ gegeben. Wählt man für jedes $ i $ eine offene Menge $ U_i \subseteq X_i $, so bilden alle kartesischen Produkte der Form $ U_1 \times U_2 \times \cdots \times U_n $ eine Basis einer Topologie auf dem Produktraum $ X_1 \times \cdots \times X_n $. Formal gilt: $$ B = \{ U_1 \times U_2 \times \cdots \times U_n \mid U_i \text{ ist offen in } X_i \text{ für alle } i \} $$

Basis der Produkttopologie

Im Fall zweier topologischer Räume wird die Produkttopologie durch kartesische Produkte offener Mengen beschrieben.

$$ B = \{ U \times V \mid U \text{ ist offen in } X,\; V \text{ ist offen in } Y \} $$

Diese Beschreibung ist korrekt, führt jedoch oft zu einer sehr großen und unübersichtlichen Basismenge.

Aus diesem Grund verwendet man in der Praxis bevorzugt eine äquivalente, aber deutlich kompaktere Konstruktion.

Sei $ B_X $ eine Basis der Topologie von $ X $ und $ B_Y $ eine Basis der Topologie von $ Y $. Dann bildet die Menge aller Produkte $ U \times V $ mit $ U \in B_X $ und $ V \in B_Y $ eine Basis der Produkttopologie auf $ X \times Y $: $$ B = \{ U \times V \mid U \in B_X,\; V \in B_Y \} $$

Diese Basismenge erzeugt die gesamte Produkttopologie auf $ X \times Y $.

Anschaulich gesprochen sind die Elemente von $ B $ die elementaren offenen Mengen der Produkttopologie, aus denen sich alle weiteren offenen Mengen durch Vereinigungen zusammensetzen lassen.

Bemerkung: Diese Konstruktion verallgemeinert sich unmittelbar auf endliche Produkte. Sind $ X_1, X_2, \dots, X_n $ topologische Räume und ist für jedes $ i $ eine Basis $ B_i $ der Topologie von $ X_i $ gegeben, so bilden alle Produkte $ U_1 \times \cdots \times U_n $ mit $ U_i \in B_i $ eine Basis der Produkttopologie auf $ X_1 \times \cdots \times X_n $: $$ B = \{ U_1 \times \cdots \times U_n \mid U_i \in B_i,\; i = 1, \dots, n \} $$

Beispiel

Zur Illustration betrachten wir zwei endliche topologische Räume:

Der Raum $ X = \{a, b\} $ mit der Topologie $ \mathcal{T}_X = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $, deren minimale Basis $ B_X = \{\{a\}, \{b\}\} $ ist.
Der Raum $ Y = \{1, 2\} $ mit der Topologie $ \mathcal{T}_Y = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} $, deren minimale Basis $ B_Y = \{\{1\}, \{2\}\} $ ist.

Um eine Basis der Produkttopologie zu erhalten, genügt es, die kartesischen Produkte der Basiselemente von $ X $ und $ Y $ zu bilden. Die Betrachtung aller offenen Mengen der beiden Räume ist nicht erforderlich.

$$ B_X = \{\{a\}, \{b\}\}, \quad B_Y = \{\{1\}, \{2\}\} $$

Die entsprechenden kartesischen Produkte sind:

$$ \{a\} \times \{1\} = \{(a, 1)\}, \quad \{a\} \times \{2\} = \{(a, 2)\} $$

$$ \{b\} \times \{1\} = \{(b, 1)\}, \quad \{b\} \times \{2\} = \{(b, 2)\} $$

Daraus ergibt sich als minimale Basis der Produkttopologie auf $ X \times Y $ die Menge

$$ B_{\text{min}} = \{\{(a, 1)\}, \{(a, 2)\}, \{(b, 1)\}, \{(b, 2)\}\} $$

Diese vier Mengen sind bereits ausreichend, um sämtliche offenen Mengen der Produkttopologie auf $ X \times Y $ zu erzeugen.

Zusammengefasst zeigt dieses Beispiel, dass man mit möglichst kleinen, elementaren offenen Mengen eine sehr kompakte Basis erhält, die dennoch die gesamte Produkttopologie vollständig beschreibt.

Beweis

Wir zeigen nun, dass die Menge $ B = \{U \times V \mid U \in B_X,\; V \in B_Y\} $ tatsächlich eine Basis der Produkttopologie auf $ X \times Y $ bildet.

Nach Voraussetzung sind $ B_X $ und $ B_Y $ Basen der Topologien von $ X $ bzw. $ Y $.

Per Definition besteht die Produkttopologie aus Vereinigungen von Mengen der Form $ U' \times V' $, wobei $ U' \subseteq X $ und $ V' \subseteq Y $ offen sind.

Um die Basiseigenschaft nachzuweisen, genügt es zu zeigen, dass jede offene Menge $ W \subseteq X \times Y $ als Vereinigung von Elementen aus $ B $ dargestellt werden kann.

Überprüfung der Basiseigenschaft

Sei $ W $ eine offene Menge der Produkttopologie und sei $ (x, y) \in W $.

Dann existiert definitionsgemäß ein offenes Rechteck $ U' \times V' \subseteq W $ mit $ U' \subseteq X $ und $ V' \subseteq Y $, so dass

$$ (x, y) \in U' \times V' \subseteq W $$

Da $ B_X $ eine Basis der Topologie von $ X $ ist, existiert ein $ U \in B_X $ mit $ x \in U \subseteq U' $. Analog existiert aufgrund der Basiseigenschaft von $ B_Y $ ein $ V \in B_Y $ mit $ y \in V \subseteq V' $.

Damit gilt

$$ (x, y) \in U \times V \subseteq U' \times V' \subseteq W $$

Folglich enthält jede offene Menge $ W $ um jeden ihrer Punkte ein Basiselement aus $ B $, das vollständig in $ W $ liegt.

Schlussfolgerung

Da jede offene Menge $ W \subseteq X \times Y $ auf diese Weise als Vereinigung von Elementen aus $ B $ dargestellt werden kann, erzeugt $ B $ tatsächlich die Produkttopologie.

Somit erfüllt die Menge $ B = \{U \times V \mid U \in B_X,\; V \in B_Y\} $ alle Voraussetzungen, um eine Basis der Produkttopologie auf $ X \times Y $ zu sein.

Der Beweis ist damit abgeschlossen.

Abschließende Bemerkungen

Abschließend seien einige zentrale und häufig verwendete Resultate zur Produkttopologie aufgeführt:

Satz über Produktsubräume
Sind $ A \subseteq X $ und $ B \subseteq Y $ Teilräume, so stimmt die auf $ A \times B $ als Teilraum von $ X \times Y $ induzierte Topologie mit der Produkttopologie überein, die aus den Teilraumtopologien von $ A $ und $ B $ gebildet wird: $$ \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Topologische Äquivalenz von Produkten
Für drei topologische Räume $ X, Y, Z $ sind die Räume $ (X \times Y) \times Z $, $ X \times (Y \times Z) $ und $ X \times Y \times Z $ zueinander homöomorph. Die Wahl der Klammerung hat keinen Einfluss auf die topologische Struktur des Produkts: $$ (X \times Y) \times Z \cong X \times (Y \times Z) \cong X \times Y \times Z $$
Satz über das Innere eines kartesischen Produkts
Für Teilmengen $ A \subseteq X $ und $ B \subseteq Y $ gilt: $$ \operatorname{Int}(A \times B) = \operatorname{Int}(A) \times \operatorname{Int}(B) $$