Unterraumtopologie und Produkttopologie

Seien $A$ und $B$ Teilmengen der topologischen Räume $X$ beziehungsweise $Y$, $$ A \subset X $$ $$ B \subset Y $$ dann stimmt die auf dem Produkt $A \times B$ definierte Topologie, sofern man $A \times B$ als Unterraum von $X \times Y$ betrachtet, genau mit der Produkttopologie auf $A \times B$ überein, die aus den von $X$ und $Y$ auf $A$ und $B$ induzierten Topologien gebildet wird: $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$

Mit $\tau_{A \times B}^{\text{sub}}$ ist dabei die Unterraumtopologie auf $A \times B$ gemeint, die durch die Produkttopologie des Raums $X \times Y$ entsteht.

Die Symbole $\tau_A^{\text{sub}}$ und $\tau_B^{\text{sub}}$ bezeichnen entsprechend die Unterraumtopologien auf $A$ und $B$, die von den Räumen $X$ beziehungsweise $Y$ induziert werden.

Der zentrale Inhalt dieser Aussage ist einfach, aber grundlegend: Beide Wege führen zur gleichen topologischen Struktur auf dem Produkt $A \times B$.

Ob man also zuerst das Produkt $X \times Y$ betrachtet und anschließend den Unterraum $A \times B$ bildet, oder ob man zunächst die Unterräume $A$ und $B$ mit ihren induzierten Topologien versieht und danach deren Produkt konstruiert, spielt keine Rolle.

In beiden Fällen erhält man exakt dieselbe Topologie auf $A \times B$.

Ein konkretes Beispiel

Um diese Aussage anschaulich zu machen, betrachten wir nun ein einfaches Beispiel.

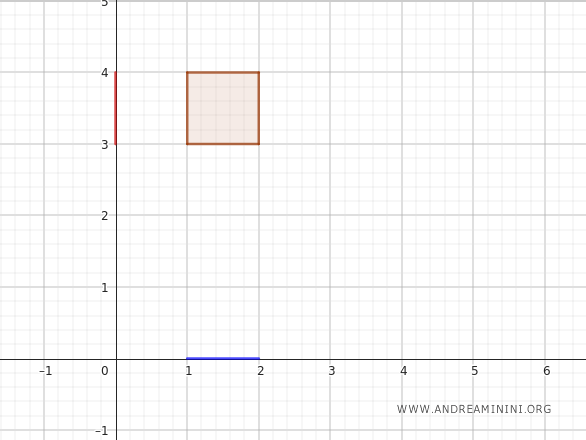
Seien $X$ und $Y$ zwei topologische Räume. Man kann sich etwa die kartesische Ebene vorstellen, wobei $X$ der x-Achse und $Y$ der y-Achse entspricht.

Es seien $A \subseteq X$ und $B \subseteq Y$ zwei Teilmengen dieser Räume.

Wir wählen zum Beispiel $A = [1, 2]$, ein Intervall auf der x-Achse, und $B = [3, 4]$, ein Intervall auf der y-Achse.

Das kartesische Produkt $A \times B$ besteht aus allen geordneten Paaren $(x, y)$ mit $x \in A$ und $y \in B$.

Geometrisch beschreibt dieses Produkt ein Rechteck in der Ebene, dessen Seiten parallel zu den Koordinatenachsen verlaufen, wobei $x$ zwischen 1 und 2 und $y$ zwischen 3 und 4 variiert.

Anschauliche Darstellung eines rechteckigen Unterraums im kartesischen Produkt

Für $A \times B$ bieten sich nun zwei naheliegende Möglichkeiten an, eine Topologie zu definieren:

Unterraumtopologie
Man betrachtet $A \times B$ als Teilmenge von $X \times Y$, also der gesamten Ebene, die mit der Produkttopologie versehen ist. Die Topologie auf $A \times B$ ergibt sich dann durch Einschränkung dieser Topologie.
Produkttopologie
Alternativ versieht man zunächst $A$ und $B$ mit den jeweils von $X$ und $Y$ induzierten Topologien und konstruiert anschließend die Produkttopologie auf $A \times B$ als Produkt dieser Topologien.

Das Ergebnis ist in beiden Fällen dasselbe.

Dieses Beispiel zeigt anschaulich, dass die gewählte Vorgehensweise keinen Einfluss auf die entstehende topologische Struktur von $A \times B$ hat.

Und so weiter...