Topologischer Teilraum

Ein topologischer Teilraum ist eine Teilmenge eines topologischen Raums, die ihre Topologie vom ursprünglichen Raum übernimmt.

Sei $ (X, T) $ ein topologischer Raum, wobei $ X $ eine Menge und $ T $ eine Familie offener Mengen ist, die die Topologie auf $ X $ definiert. Sei $ Y \subseteq X $. Dann wird die Teilraumtopologie auf $ Y $ definiert durch: \[ T_Y = \{ U \cap Y \mid U \in T \} \]

Mit anderen Worten: Eine Menge $ V \subseteq Y $ gilt genau dann als offen in der Teilraumtopologie, wenn sie als Schnittmenge von $ Y $ mit einer offenen Menge $ U $ des Ausgangsraums $ X $ dargestellt werden kann.

Alle offenen Mengen in der Teilraumtopologie von $ Y $ sind somit von der Form $ U \cap Y $, wobei $ U $ in $ X $ offen ist.

$$ V_{offen \ in \ Y} = U \cap Y $$

Analog dazu sind alle abgeschlossenen Mengen in der Teilraumtopologie von $ Y $ von der Form $ C \cap Y $, wobei $ C $ in $ X $ abgeschlossen ist.

$$ V_{abgeschlossen \ in \ Y} = C \cap Y $$

Hinweis. Offene Mengen in der Teilraumtopologie $ Y $ müssen nicht notwendigerweise offen im gesamten Raum $ X $ sein. Es kann vorkommen, dass eine Menge in $ Y $ offen, aber in $ X $ geschlossen ist, oder umgekehrt. Manche Mengen können sowohl in $ Y $ als auch in $ X $ offen oder geschlossen sein. Außerdem gibt es sogenannte „clopen"-Mengen, die zugleich offen und geschlossen sind. Ein Beispiel dafür wird im ersten Abschnitt dieser Notizen behandelt und erläutert.

Beispiel
Eigenschaften der Teilraumtopologie
Bemerkungen

Beispiel

Betrachten wir den topologischen Raum $ \mathbb{R} $ mit der Standardtopologie, bei der offene Mengen offene Intervalle sind.

Sei $ Y = [0, 1] $ eine Teilmenge von $ \mathbb{R} $.

Die Teilraumtopologie auf $ Y $ besteht aus allen Mengen der Form:

$$ U \cap [0, 1] $$

wobei $ U $ eine offene Menge in $ \mathbb{R} $ ist.

Zum Beispiel ist die Menge (-1, 0.5) offen im topologischen Raum $ \mathbb{R} $.

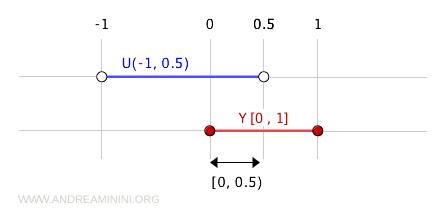
Beispiel eines Teilraums

Die Schnittmenge von (-1, 0.5) mit $ Y = [0, 1] $ ist eine offene Menge in der Teilraumtopologie auf $ Y $:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Das Intervall $ [0, 0.5) $ ist also offen im Teilraum $ Y $.

Das Intervall $ [0, 0.5] $ hingegen ist in der Teilraumtopologie auf $ Y $ abgeschlossen, da es als Schnitt der abgeschlossenen Menge [-1, 0.5] in $ X $ mit $ Y $ dargestellt werden kann:

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Zusammenfassend erbt der Teilraum $ Y $ eine Topologie vom Ausgangsraum $ X $, bei der die offenen Mengen in $ Y $ genau die Schnittmengen von $ Y $ mit den offenen Mengen von $ X $ sind.

Hinweis. Mengen wie [0,a) oder (a,1], wobei 0<a<1, sind in der Standardtopologie von $ \mathbb{R} $ nicht offen, wohl aber in der Teilraumtopologie. Sie lassen sich nämlich als Schnittmengen von $ Y = [0,1] $ mit einer offenen Menge in $ \mathbb{R} $ darstellen. Zum Beispiel gilt: $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ Das Intervall [0,0.5) ist daher offen im Teilraum $ Y $, obwohl es in der Standardtopologie von $ \mathbb{R} $ nicht offen ist.

Es gibt auch Mengen, die sowohl in der Teilraumtopologie von $ Y $ als auch in $ X $ offen sind, wie etwa (0.2, 0.8).

Ebenso gibt es Mengen, die sowohl in $ Y $ als auch in $ X $ abgeschlossen sind, beispielsweise [0.2, 0.8].

In der Teilraumtopologie $ Y = [0, 1] $ ist die Menge $ [0, 1] $ sowohl offen als auch geschlossen.

Offenheit
Um zu zeigen, dass $ [0, 1] $ im Teilraum $ Y $ offen ist, genügt es, eine offene Menge $ U $ in $ \mathbb{R} $ zu finden, für die $ U \cap Y = [0, 1] $ gilt. Wählen wir $ U = \mathbb{R} $, das offen in $ \mathbb{R} $ ist, ergibt sich: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Damit ist $ [0, 1] $ offen im Teilraum $ Y $.
Abgeschlossenheit
Um zu zeigen, dass $ [0, 1] $ im Teilraum $ Y $ abgeschlossen ist, suchen wir eine abgeschlossene Menge $ C $ in $ \mathbb{R} $, sodass $ C \cap Y = [0, 1] $. Wählen wir $ C = [0, 1] $, das in $ \mathbb{R} $ abgeschlossen ist, so gilt: $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Somit ist $ [0, 1] $ abgeschlossen in $ Y $.
Hinweis: Alternativ lässt sich die Abgeschlossenheit auch zeigen, indem man das Komplement von $ [0, 1] $ in $ Y $ betrachtet. Dieses ist die leere Menge, die in jeder Topologie offen ist. Da das Komplement einer offenen Menge abgeschlossen ist, folgt, dass $ [0, 1] $ abgeschlossen in $ Y $ ist.

Folglich ist $ [0, 1] $ in der Teilraumtopologie $ Y = [0, 1] $ sowohl offen als auch geschlossen. Solche Mengen nennt man „clopen", eine Zusammensetzung aus „closed" und „open".

Beispiel 2

Betrachten wir die Standardtopologie auf der Menge der reellen Zahlen $ \mathbb{R} $.

In dieser Topologie ist jedes Intervall (a,b) mit a < b offen.

Ein typischer topologischer Teilraum von $ \mathbb{R} $ ist die Menge der ganzen Zahlen $ \mathbb{Z} $, denn jede ganze Zahl lässt sich als Schnittmenge offener Intervalle in $ \mathbb{R} $ darstellen.

Zum Beispiel ergibt sich die ganze Zahl 7 als Schnitt der offenen Menge (6.5,7.5) in $ \mathbb{R} $ mit der Menge $ \mathbb{Z} $:

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

Auf dieselbe Weise kann man jede andere ganze Zahl erhalten. Damit ist jedes einzelne Element von $ \mathbb{Z} $ offen in der Teilraumtopologie auf $ \mathbb{Z} $.

Ebenso ist jede Teilmenge von $ \mathbb{Z} $ offen in dieser Teilraumtopologie.

Zum Beispiel gilt für die offene Menge (5.5,8.5):

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Dieser topologische Teilraum auf $ \mathbb{Z} $ wird auch als diskrete Topologie bezeichnet.

Hinweis: Die diskrete Topologie auf $ \mathbb{Z} $ ist nicht selbst ein Teilraum der Standardtopologie auf $ \mathbb{R} $, sondern eine eigenständige Topologie. Allerdings ist die von $ \mathbb{Z} $ aus der Standardtopologie auf $ \mathbb{R} $ geerbte Teilraumtopologie zur diskreten Topologie auf $ \mathbb{Z} $ äquivalent.

Beispiel 3

Betrachten wir den dreidimensionalen euklidischen Raum $ \mathbb{R}^3 $ mit der Standardtopologie, in der offene Mengen als Vereinigungen offener Kugeln definiert sind.

Wir nehmen nun die Einheitskugeloberfläche $ S^2 $, definiert als die Menge aller Punkte in $ \mathbb{R}^3 $, deren Abstand vom Ursprung gleich 1 ist:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

Die Teilraumtopologie auf $ S^2 $ wird folgendermaßen definiert:

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ ist offen in } \mathbb{R}^3 \} $$

Anders gesagt: Eine Menge $ V \subseteq S^2 $ ist genau dann offen in der Teilraumtopologie, wenn sie als Schnittmenge von $ S^2 $ mit einer offenen Menge $ U $ in $ \mathbb{R}^3 $ dargestellt werden kann.

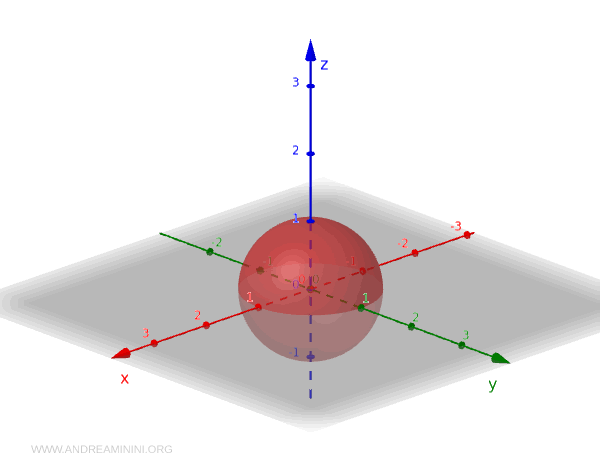
Kugeloberfläche als Teilraum von R3

Einige Beispiele für offene Mengen in $ S^2 $:

Vereinigung offener Mengen in $ \mathbb{R}^3 $
Betrachten wir die offene Menge $ U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} $.
Ihre Schnittmenge mit $ S^2 $ ist: $$ U \cap S^2 = S^2 $$ denn für alle Punkte auf $ S^2 $ gilt $ x^2 + y^2 + z^2 = 1 < 2 $. Daher ist $ S^2 $ offen in seiner eigenen Teilraumtopologie.
Ein Teil der Kugeloberfläche
Betrachten wir nun die Menge $ U = \{ (x, y, z) \in \mathbb{R}^3 \mid z > 0 \} $.
Ihre Schnittmenge mit $ S^2 $ ist $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$.
Diese Menge entspricht der oberen Halbkugel und ist offen in der Teilraumtopologie $ T_{S^2} $.
Offene Mengen und ihre Stabilität
Sowohl die leere Menge $ \emptyset $ als auch $ S^2 $ selbst sind offen in $ S^2 $.
- Der Schnitt endlich vieler offener Mengen in $ S^2 $ ist wieder offen in $ S^2 $.
- Beliebige Vereinigungen offener Mengen in $ S^2 $ sind ebenfalls offen in $ S^2 $.

Zusammenfassend lässt sich sagen: Die Kugeloberfläche $ S^2 $ erbt als Teilraum von $ \mathbb{R}^3 $ die Standardtopologie des euklidischen Raums. Die offenen Mengen in $ S^2 $ entstehen durch die Schnittmenge von $ S^2 $ mit offenen Mengen in $ \mathbb{R}^3 $.

Eigenschaften der Teilraumtopologie

Die Teilraumtopologie besitzt die folgenden grundlegenden Eigenschaften:

Offene Mengen
Alle offenen Mengen in $ Y $ sind von der Form $ U \cap Y $, wobei $ U $ offen in $ X $ ist.
Leere Menge und Gesamtraum
Sowohl die leere Menge $ \emptyset $ als auch $ Y $ selbst sind immer offen in $ Y $:
- $ \emptyset $ ist offen, da $ \emptyset = \emptyset \cap Y $.
- $ Y $ ist offen, da $ Y = X \cap Y $.
Endliche Durchschnitte
Der Schnitt einer endlichen Anzahl offener Mengen in $ Y $ ist wieder offen in $ Y $. Wenn $ V_1, \ldots, V_n $ offen in $ Y $ sind, gilt: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ wobei jedes $ U_i $ offen in $ X $ ist. Da der endliche Schnitt offener Mengen in $ X $ offen bleibt, ist auch der resultierende Schnitt offen in $ Y $.
Beliebige Vereinigungen
Eine beliebige Vereinigung offener Mengen in $ Y $ ist ebenfalls offen in $ Y $. Wenn für jedes $ \alpha $ aus einer Indexmenge $ I $ gilt, dass $ V_\alpha $ offen in $ Y $ ist, dann: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ wobei jedes $ U_\alpha $ offen in $ X $ ist. Da Vereinigungen offener Mengen in $ X $ offen sind, bleibt auch die Vereinigung offen in $ Y $.

Bemerkungen

Einige ergänzende Beobachtungen zu Teilräumen:

Die Standardtopologie auf einem Teilraum $ Y \subseteq \mathbb{R}^n $ fällt mit der von $ \mathbb{R}^n $ geerbten Teilraumtopologie zusammen.
Beispiel. Betrachten wir die Menge $ Y = [-1,0) \cup (0,1] $, eine Teilmenge von $ \mathbb{R} $. In der Standardtopologie auf $ Y $ sind die Intervalle [-1,0) und (0,1] beide offen, da sie als Schnittmengen von $ Y $ mit offenen Mengen in der Standardtopologie auf $ \mathbb{R} $ dargestellt werden können. Zum Beispiel gilt für die offenen Mengen (-1.5,0.5) und (0,1.5) in $ \mathbb{R} $: $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Somit ist die Standardtopologie auf $ Y $ äquivalent zur Teilraumtopologie der Standardtopologie auf $ \mathbb{R} $. In diesem Fall sind die Intervalle [-1,0) und (0,1] auch abgeschlossen in der Standardtopologie auf $ Y $, da das Komplement der offenen Menge [-1,0) gleich (0,1] ist und umgekehrt. Daher sind beide Mengen zugleich offen und abgeschlossen („clopen") in der Standardtopologie auf $ Y $.
Basissatz der Teilraumtopologie
Dieser Satz besagt: Ist $ B_X $ eine Basis der Topologie eines topologischen Raums $ X $ und $ Y \subset X $, so bildet die Menge aller Schnitte $ B \cap Y $ eine Basis $ B_Y $ der Teilraumtopologie auf $ Y $: $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$

Und so weiter.