Inneres einer Menge

In einem topologischen Raum $ X $ bezeichnet man das Innere einer Menge $ A $ als die Vereinigung aller offenen Teilmengen, die vollständig in $ A $ enthalten sind. Es wird üblicherweise mit $ \text{Int}(A) $ oder $ A^\circ $ notiert.

Das Innere ist die größte offene Teilmenge, die vollständig in $ A $ liegt.

Es existiert keine offene Teilmenge von $ A $, die größer wäre als ihr Inneres.

Bemerkung: Aus der Definition folgt unmittelbar, dass das Innere einer Menge als Vereinigung offener Mengen immer selbst offen ist.

Formal ist das Innere von $ A $ die Menge aller Punkte in $ A $, die eine offene Umgebung besitzen, die vollständig in $ A $ enthalten ist.

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ ist offen in } X \} $$

Ein Punkt $ x $ gehört genau dann zum Inneren von $ A $, wenn ein offenes $ U $ existiert, für das $ x \in U \subseteq A $ gilt.

Wichtig ist, dass das Innere einer Menge $ A $ von der auf $ X $ gewählten Topologie abhängt und nicht von $ A $ allein. Je nach Topologie kann das Innere unterschiedlich ausfallen.

Konkretes Beispiel
Theorem über das Innere einer Menge
Eigenschaften des Inneren
Bemerkungen

Konkretes Beispiel

Betrachten wir die Menge $ A = [0,1] $ im Raum $ \mathbb{R} $ mit der üblichen Topologie.

Dieses Intervall enthält alle reellen Zahlen zwischen 0 und 1 einschließlich der Randpunkte.

In diesem Fall ist das Innere von $ A $ das offene Intervall $ (0,1) $.

$$ \text{Int}(A) = (0,1) $$

Es ist die größte offene Teilmenge von $ A $, da die Randpunkte 0 und 1 zu keinem offenen Intervall gehören, das vollständig in $ A $ enthalten ist.

Beispiel 2

Betrachten wir nun $ A = [0,1) $ im selben Raum mit der üblichen Topologie.

Diese Menge enthält alle reellen Zahlen von 0 (inklusive) bis 1 (exklusive), also ein links abgeschlossenes und rechts offenes Intervall.

Trotzdem gilt für das Innere weiterhin $ (0,1) $.

\[ \text{Int}(A) = (0,1) \]

Das Innere ist per Definition die Vereinigung aller offenen Teilmengen von $ A $, und die größte von ihnen ist $ (0,1) $.

Bemerkung: In der Standardtopologie von $ \mathbb{R} $ sind offene Mengen Vereinigungen offener Intervalle. Da 0 in keinem solchen Intervall liegt, das vollständig in $ [0,1) $ enthalten ist, gehört dieser Punkt nicht zum Inneren.

Beispiel 3

Betrachten wir erneut $ A = [0,1) $, diesmal in einem Raum $ X $ mit der diskreten Topologie.

In dieser Topologie ist jede Teilmenge offen.

Daher besitzt jeder Punkt von $ A $ eine offene Umgebung, die vollständig in $ A $ liegt.

In der diskreten Topologie auf $ \mathbb{R} $ ist jede Teilmenge offen, unabhängig davon, ob sie ein Intervall, eine endliche Menge oder eine beliebige Vereinigung darstellt. Mengen wie $ (0,0{,}5) $, $ (0{,}25,0{,}75) $, $ (0,1) $, $ [0,0{,}25] $, die leere Menge oder auch $ [0,1) $ selbst sind daher alle offen.

Folglich ist die Menge $ A $ offen.

Damit ist das Innere von $ A $ identisch mit $ A $:

$$ \text{Int}(A) = A = [0,1) $$

In einer diskreten Topologie stimmt das Innere jeder Menge mit der Menge selbst überein.

Bemerkung: Dieses Beispiel zeigt klar, wie stark die Wahl der Topologie die Begriffe Umgebung und Inneres beeinflusst. Das Innere hängt nicht von der Menge $ A $ als solcher ab, sondern von der zugrunde liegenden Topologie des Raumes $ X $.

Beispiel 4

Betrachten wir nun den topologischen Raum $ X = \{a, b, c\} $ mit der diskreten Topologie.

In diesem Raum ist jede Teilmenge offen:

Per Definition sind $ \emptyset $ und $ \{a, b, c\} $ offen.
Auch die Singletons $ \{a\} $, $ \{b\} $, $ \{c\} $ sind offen, da jeder Punkt eine offene Menge bildet.
Ebenso sind die zweielementigen Teilmengen $ \{a, b\} $, $ \{a, c\} $, $ \{b, c\} $ offen.

Betrachten wir $ A = \{b, c\} $.

Das Innere von $ A $ ist die Vereinigung aller offenen Teilmengen, die vollständig in $ A $ enthalten sind.

In diesem Fall sind dies $ \{b\} $, $ \{c\} $ und $ \{b, c\} $ selbst.

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Damit ergibt sich $ \text{Int}(A) = A $.

Bemerkung: Dieses Resultat gilt für jede Teilmenge $ S \subseteq X $ in einer diskreten Topologie. Da jede Teilmenge offen ist, folgt stets $ \text{Int}(S) = S $.

Theorem über das Innere einer Menge

In einem topologischen Raum $ X $ gilt für eine Teilmenge $ S $ und einen Punkt $ y \in X $: Man sagt, $ y $ gehört zum Inneren von $ S $, notiert $ \operatorname{Int}(S) $, wenn es eine offene Menge $ U $ gibt, für die $ y \in U \subseteq S $ gilt. Formal: $$ y \in \text{Int}(S) \iff \exists \ U \text{ offen mit } y \in U \subseteq S $$

Ein Punkt $ y $ ist also genau dann ein innerer Punkt von $ S $, wenn er eine offene Umgebung besitzt, die vollständig in $ S $ liegt.

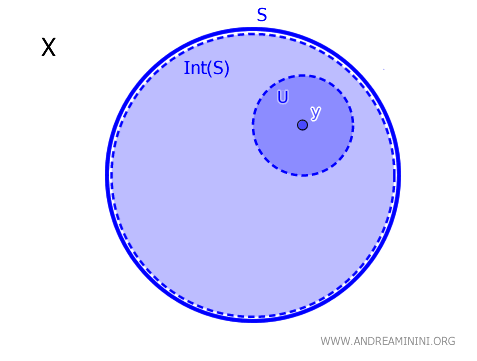
visuelles Beispiel

Dieses Theorem liefert ein notwendiges und hinreichendes Kriterium, um festzustellen, ob ein Punkt $ y $ zum Inneren einer Menge $ S $ in einem topologischen Raum $ X $ gehört.

Beweis

Notwendigkeit: Gilt $ y \in \operatorname{Int}(S) $, so existiert per Definition eine offene Menge $ U \subseteq X $ mit $ y \in U \subseteq S $. Dies folgt unmittelbar aus der Definition des Inneren.
Hinreichend: Existiert ein offenes $ U $ mit $ y \in U \subseteq S $, gehört $ y $ definitionsgemäß zum Inneren von $ S $, da dieses die Vereinigung aller offenen Teilmengen von $ S $ ist.

Bemerkung: Dieses Theorem ist zentral, da es die Begriffe offene Menge und innerer Punkt eindeutig miteinander verknüpft. Es spielt eine grundlegende Rolle in der Untersuchung von Stetigkeit und weiteren Kernbegriffen der Topologie.

Beispiel

Betrachten wir die Menge $ A = [1,3] $, also das abgeschlossene Intervall von 1 bis 3 im Raum $ \mathbb{R} $ mit der üblichen Topologie.

$$ A = [1,3] $$

Dieses Intervall umfasst alle reellen Zahlen zwischen 1 und 3 einschließlich der Randpunkte.

Um das Innere zu bestimmen, wenden wir das zuvor formulierte Theorem an.

Bestimmung des Inneren von $ A $

Wir suchen eine offene Menge $ U $, für die $ U \subseteq A $ gilt und deren Punkte alle zu $ \operatorname{Int}(A) $ gehören.

Wahl von $ U $
Wir wählen $ U = (1,3) $, das offene Intervall ohne Randpunkte. Dieses Intervall ist in der Standardtopologie von $ \mathbb{R} $ offen.
Überprüfung der Inklusion $ U \subseteq A $
Alle Punkte von $ (1,3) $ liegen in $ [1,3] $, während die Randpunkte $ 1 $ und $ 3 $ nicht zu $ U $ gehören.

Damit ist $ U $ eine offene Teilmenge von $ A $, deren Punkte sämtlich zu $ \operatorname{Int}(A) $ gehören. Also ist das Innere von $ A $ genau $ (1,3) $.

Bemerkung: Die Randpunkte 1 und 3 gehören nicht zu $ \operatorname{Int}(A) $, da kein offenes Intervall existiert, das vollständig in $ A $ liegt und sie einschließt. Dies veranschaulicht anschaulich die Aussage des Theorems.

Eigenschaften des Inneren

Im Folgenden sind grundlegende Eigenschaften des Inneren in einem topologischen Raum aufgeführt. Sie machen die Wechselwirkungen zwischen topologischen Operationen wie Innerem, Abschluss, Vereinigung und Durchschnitt deutlich. Einige dieser Eigenschaften können auf den ersten Blick überraschend erscheinen.

Eigenschaft der Vereinigung der Inneren
Die Vereinigung der Inneren zweier Mengen ist stets im Inneren der Vereinigung enthalten, und diese Inklusion kann strikt sein. $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Eigenschaft des Durchschnitts der Inneren
Das Innere des Durchschnitts zweier Mengen ist gleich dem Durchschnitt ihrer Inneren. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
Beziehung zwischen dem Inneren des Komplements und dem Komplement des Abschlusses
Es gilt die Identität: $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
Beziehung zwischen dem Abschluss des Komplements und dem Komplement des Inneren
Ebenso gilt: $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Bemerkungen

Die folgenden Hinweise ergänzen das Verständnis des Inneren einer Menge:

Ist $ U $ offen in $ X $ und gilt $ U \subseteq A $, dann gilt $ U \subseteq \operatorname{Int}(A) $
Jedes offene Teilset von $ A $ liegt im Inneren von $ A $, da dieses per Definition die größte offene Teilmenge von $ A $ darstellt.
Gilt $ A \subseteq B $, so gilt auch $ \operatorname{Int}(A) \subseteq \operatorname{Int}(B) $
Die Bildung des Inneren ist monoton: aus der Inklusion zweier Mengen folgt stets die Inklusion ihrer Inneren.
Eine Menge $ A $ ist genau dann offen, wenn $ A = \operatorname{Int}(A) $
Dies ist ein klassisches Charakteristikum offener Mengen: Eine Menge ist offen, wenn jeder ihrer Punkte eine offene Umgebung besitzt, die vollständig in ihr enthalten ist.
Bestimmung des Inneren einer Menge mit R
Die Programmiersprache R, weit verbreitet in Analyse und Statistik, bietet effiziente Werkzeuge zur Bestimmung und Visualisierung des Inneren einer Menge.

Und so weiter.