Vereinigung der Inneren zweier Mengen
Wenn wir zwei Mengen \( A \) und \( B \) betrachten, dann gilt: Die Vereinigung ihrer Inneren liegt immer vollständig im Inneren ihrer Vereinigung. Formal ausgedrückt: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Diese Beziehung ist jedoch keine Gleichheit im allgemeinen Fall.
Das bedeutet: Das Innere der Vereinigung ist immer mindestens so groß wie die Vereinigung der beiden Inneren, aber manchmal sogar größer.
Die beiden Mengen müssen also nicht immer identisch sein. Es gilt nicht automatisch:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Manchmal ist die Inklusion echt, also:
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Dieses scheinbar kleine Detail ist entscheidend, wenn man verstehen möchte, wie sich Mengen und ihre Inneren im Rahmen der Topologie zueinander verhalten.
Ein einfaches Beispiel
Betrachten wir zwei offene Intervalle in \(\mathbb{R}\):
$$ A = (0, 2) \qquad B = (1, 3) $$
Das Innere eines offenen Intervalls ist das Intervall selbst, also:
$$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (1, 3) $$
Ihre Vereinigung ergibt:
$$ (0, 2) \cup (1, 3) = (0, 3) $$
Auch die Vereinigung der beiden Mengen selbst liefert dasselbe Ergebnis:
$$ A \cup B = (0, 3) $$
Somit ist:
$$ \text{Int}(A \cup B) = (0, 3) $$
In diesem Fall sind die beiden Seiten gleich:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Ein Gegenbeispiel
Nehmen wir nun zwei abgeschlossene Intervalle: $$ A = [0, 2] \qquad B = [2, 3] $$ Ihre Inneren sind: $$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (2, 3) $$ Die Vereinigung lautet \( A \cup B = [0, 3] \), deren Inneres: $$ \text{Int}(A \cup B) = (0, 3) $$ Wir haben also: $$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$ Doch der Punkt \( 2 \) gehört zum Inneren der Vereinigung, $$ 2 \in (0, 3) $$ nicht aber zu den einzelnen Inneren: $$ 2 \not\in (0, 2), \quad 2 \not\in (2, 3) $$ Somit gilt: $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ Dieses Beispiel zeigt, dass die Inklusion echt sein kann.
Ein weiteres Beispiel
Betrachten wir zwei disjunkte offene Intervalle:
$$ A = (0, 1) \qquad B = (2, 3) $$
Da beide Intervalle bereits offen sind, gilt:
$$ \text{Int}(A) = (0, 1) \qquad \text{Int}(B) = (2, 3) $$
und daher:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
Die Vereinigung ist ebenfalls offen, daher bleibt das Innere unverändert:
$$ \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$
Hier gilt also wieder Gleichheit. In \(\mathbb{R}\) sehen wir also: Die Vereinigung der Inneren ist immer im Inneren der Vereinigung enthalten, aber Gleichheit tritt nur in bestimmten Fällen auf. Sobald sich die Randpunkte überlappen, wird die Inklusion streng.
Ein Beispiel in der Ebene
Nun betrachten wir zwei Mengen \( A \) und \( B \) in der Ebene \(\mathbb{R}^2\) mit der Standardtopologie.
Beide seien offene Kreisscheiben mit Radius \( 1 \), deren Mittelpunkte bei \( (0, 0) \) und \( (0{,}5, 0) \) liegen. Sie überlappen sich teilweise:
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0{,}5)^2 + y^2 < 1 \} $$
Da beide Mengen offen sind, gilt:
$$ \text{Int}(A) = A \qquad \text{Int}(B) = B $$
Die Vereinigung der Inneren entspricht der Vereinigung der beiden Scheiben:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
Diese Vereinigung bildet eine zusammenhängende Fläche mit einer überlappenden Zone.
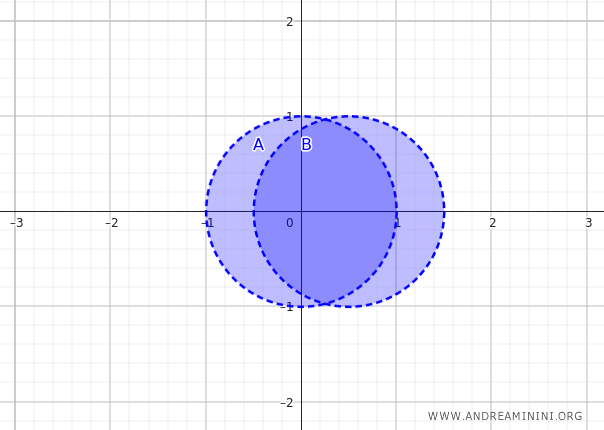
Das Innere der Vereinigung \( A \cup B \) enthält alle Punkte, die eine Umgebung besitzen, die vollständig in \( A \cup B \) liegt. Auch hier gilt:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Warum das immer gilt
Um diese Eigenschaft zu verstehen, erinnern wir uns an die Definition des Inneren einer Menge.
Das Innere einer Menge \( X \), bezeichnet mit \( \text{Int}(X) \), besteht aus allen Punkten \( x \in X \), die eine offene Umgebung besitzen, die vollständig in \( X \) enthalten ist.
Sei nun \( x \in \text{Int}(A) \cup \text{Int}(B) \). Dann gilt: \( x \) gehört entweder zum Inneren von \( A \) oder zum Inneren von \( B \).
- Ist \( x \in \text{Int}(A) \), so existiert eine offene Menge \( U_x \) mit \( x \in U_x \subseteq A \).
- Ist \( x \in \text{Int}(B) \), so existiert eine offene Menge \( V_x \) mit \( x \in V_x \subseteq B \).
Da sowohl \( A \) als auch \( B \) Teilmengen von \( A \cup B \) sind, gilt in beiden Fällen \( U_x \subseteq A \cup B \) bzw. \( V_x \subseteq A \cup B \). Damit folgt automatisch \( x \in \text{Int}(A \cup B) \).
Also gilt immer:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Damit ist gezeigt, warum diese Eigenschaft unabhängig von der konkreten Wahl der Mengen immer erfüllt ist.