Der Abschluss einer Menge in der Topologie

Der Abschluss einer Menge \( A \) in einem topologischen Raum \( X \) ist der Schnitt aller abgeschlossenen Mengen, die \( A \) enthalten. Diese Menge wird mit \( \text{Cl}(A) \) bezeichnet.

Einfach gesagt: Der Abschluss von \( A \) ist die kleinste abgeschlossene Menge, die \( A \) vollständig einschließt.

Es gibt keine abgeschlossene Menge, die \( A \) enthält und dabei kleiner als ihr Abschluss ist. Der Abschluss fasst also alle Punkte zusammen, die man nicht „verliert", wenn man \( A \) zu einer abgeschlossenen Menge ergänzt.

Hinweis: Diese Eigenschaft ergibt sich direkt aus der Definition. Der Abschluss wird als Schnitt aller abgeschlossenen Mengen gebildet, die \( A \) enthalten. Damit ist er die kleinste abgeschlossene Menge, die \( A \) umfassen kann - bestehend aus allen Punkten, die diesen Mengen gemeinsam sind.

Formal schreibt man:

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ und } C \text{ ist abgeschlossen in } X \} $$

Das Symbol \( \bigcap \) steht hier für die Schnittmenge aller abgeschlossenen Mengen \( C \), die \( A \) enthalten.

Der Abschluss von \( A \) besteht aus den Punkten von \( A \) selbst und aus allen Häufungspunkten von \( A \) im Raum \( X \).

Hinweis: Der Abschluss hängt immer von der Topologie des Raums ab, nicht von den inneren Eigenschaften der Menge selbst. In verschiedenen topologischen Räumen kann ein und dieselbe Menge daher unterschiedliche Abschlüsse haben.

Beispiel 1: Ein offenes Intervall in den reellen Zahlen

Betrachten wir \( A = (0,1) \) im Raum \( \mathbb{R} \) mit der Standardtopologie.

Das Intervall \( (0,1) \) enthält alle Zahlen zwischen 0 und 1, aber nicht die Randpunkte.

In diesem Fall gilt:

$$ \text{Cl}(A) = [0,1] $$

Der Abschluss enthält also das ursprüngliche Intervall und zusätzlich die beiden Randpunkte 0 und 1, die als Häufungspunkte von \( A \) gelten.

Hinweis: In der Standardtopologie auf \( \mathbb{R} \) ist eine Menge genau dann abgeschlossen, wenn sie alle ihre Häufungspunkte enthält. Ein Punkt \( x \) heißt Häufungspunkt, wenn jede Umgebung von \( x \) mindestens einen anderen Punkt aus \( A \) enthält. Zum Beispiel ergibt der Schnitt der abgeschlossenen Intervalle [0,2] und [-1,1] genau [0,1]: $$ [0,2] \cap [-1,1] = [0,1] $$ Kein kleineres abgeschlossenes Intervall enthält \( (0,1) \).

Beispiel 2: Ein halboffenes Intervall

Nun betrachten wir \( A = [0,1) \) in \( \mathbb{R} \) mit der Standardtopologie.

Dieses halboffene Intervall enthält alle Zahlen von 0 (inklusive) bis 1 (exklusive).

Auch hier ergibt sich:

$$ \text{Cl}(A) = [0,1] $$

Der Punkt 0 gehört bereits zu \( A \), während 1 ein Häufungspunkt ist, der hinzugefügt wird, um \( A \) abzuschließen. Das Ergebnis ist das abgeschlossene Intervall [0,1].

Hinweis: Dieses Beispiel zeigt anschaulich, dass der Abschluss immer alle Häufungspunkte einer Menge enthält. So ergibt auch hier der Schnitt der Intervalle [0,2] und [-1,1] wieder [0,1]. $$ [0,2] \cap [-1,1] = [0,1] $$

Beispiel 3: Abschluss in der diskreten Topologie

Betrachten wir nun die gleiche Menge \( A = [0,1) \), diesmal in einem Raum \( X \) mit der diskreten Topologie.

In einer diskreten Topologie ist jede Teilmenge gleichzeitig offen und abgeschlossen.

• Offenheit: Jede Teilmenge von \( X \) ist offen. Wenn also \( A \subset X \), ist \( A \) offen.
• Abgeschlossenheit: Da das Komplement jeder Teilmenge offen ist, ist auch \( A \) selbst abgeschlossen.

Damit ist jede Menge offen und abgeschlossen zugleich (engl. *clopen*).

Folglich stimmt der Abschluss von \( A \) hier genau mit \( A \) selbst überein:

$$ \text{Cl}(A) = [0,1) $$

Die kleinste abgeschlossene Menge, die \( A \) enthält, ist also einfach \( A \) selbst.

Hinweis: Dieses Beispiel zeigt, wie die gewählte Topologie den Abschluss einer Menge vollständig verändern kann. Die Abgeschlossenheit hängt von der Struktur des Raums \( X \) ab, nicht von der Menge selbst.

Beispiel 4: Ein diskreter Raum mit endlich vielen Punkten

Betrachten wir den topologischen Raum \( X = \{a, b, c\} \) mit der diskreten Topologie.

In diesem Raum ist jede Teilmenge offen:

• Die Mengen \( \emptyset \) und \( \{a, b, c\} \) sind per Definition offen.
• Die Einelementmengen \( \{a\} \), \( \{b\} \) und \( \{c\} \) sind offen.
• Auch Kombinationen wie \( \{a,b\} \), \( \{a,c\} \) oder \( \{b,c\} \) sind offen.

Da jedes Komplement ebenfalls offen ist, sind alle Teilmengen gleichzeitig offen und abgeschlossen.

Nehmen wir \( A = \{b, c\} \). Diese Menge ist offen und abgeschlossen zugleich, da ihr Komplement \( X/A = \{a\} \) offen ist.

Der Abschluss von \( A \) ist der Schnitt aller abgeschlossenen Mengen, die \( A \) enthalten. In diesem Fall ist keine Erweiterung nötig:

\[ \text{Cl}(A) = \{b, c\} \]

In einer diskreten Topologie ist jede Menge bereits abgeschlossen, daher gilt immer \( \text{Cl}(A) = A \).

Hinweis: Die abgeschlossenen Mengen, die \( A \) enthalten, sind \( \{b, c\} \) und \( \{a, b, c\} \). $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ Der Schnitt ergibt genau \( A \), also \( \text{Cl}(A) = A \).

Der Abschluss einer Menge - Grundlagen und Bedeutung

In einem topologischen Raum \( X \) gehört ein Punkt \( y \) genau dann zum Abschluss einer Teilmenge \( S \), bezeichnet mit \( \text{Cl}(S) \), wenn jede offene Menge \( U \), die \( y \) enthält, \( S \) schneidet: $$ y \in \text{Cl}(S) \iff \forall \, U \text{ offen mit } y \in U, \ U \cap S \neq \emptyset. $$

Einfach gesagt: Ein Punkt \( y \in X \) liegt im Abschluss von \( S \), wenn jede offene Umgebung von \( y \) mindestens einen Punkt aus \( S \) enthält. Kein offenes Gebiet um \( y \) ist also völlig frei von Punkten aus \( S \).

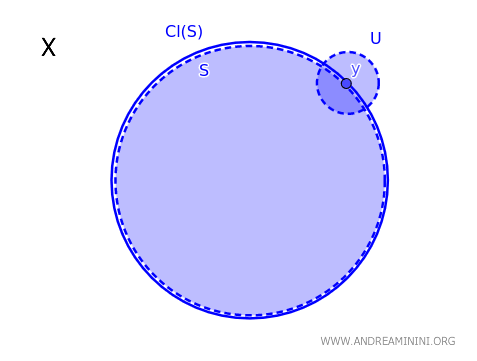
Dieser Satz ist eine der zentralen Aussagen der Topologie. Er beschreibt, wann ein Punkt „an“ einer Menge liegt - also entweder Teil der Menge selbst ist oder ihr beliebig nahekommt.

Beweisidee

• Notwendige Bedingung: Liegt \( y \) im Abschluss \( \text{Cl}(S) \), dann schneidet jede offene Menge, die \( y \) enthält, die Menge \( S \). Das gilt, weil der Abschluss alle Punkte von \( S \) und alle ihre Häufungspunkte umfasst. Ein Häufungspunkt ist ein Punkt, in dessen jeder Umgebung mindestens ein Punkt von \( S \) liegt, der mit ihm identisch oder verschieden sein kann.
• Hinreichende Bedingung: Wenn jede offene Umgebung von \( y \) Punkte aus \( S \) enthält, dann ist \( y \) entweder selbst ein Element von \( S \) oder ein Häufungspunkt davon. In beiden Fällen gehört \( y \) zum Abschluss \( \text{Cl}(S) \).

Hinweis: Dieser Zusammenhang zwischen Offenheit und Abgeschlossenheit ist eines der Grundprinzipien der Topologie. Er spielt eine entscheidende Rolle bei der Definition der Stetigkeit, bei der Beschreibung von Konvergenz und in vielen zentralen Beweisen der Disziplin.

Ein Beispiel zur Veranschaulichung

Betrachten wir das offene Intervall \( A = (0, 2) \) in den reellen Zahlen \( \mathbb{R} \) mit der Standardtopologie.

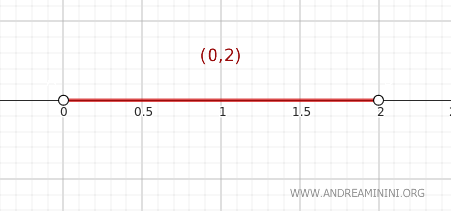
Wir wollen prüfen, ob der Punkt \( y = 2 \) zum Abschluss \( \text{Cl}(A) \) gehört.

Nach dem Satz gilt: \( y \in \text{Cl}(A) \) genau dann, wenn jede offene Menge, die \( y \) enthält, die Menge \( A \) schneidet.

1. Untersuchung der Umgebungen von \( y \): Jedes offene Intervall um \( y = 2 \), etwa \( (1{,}9, 2{,}1) \) oder \( (1{,}99, 2{,}01) \), enthält Punkte aus \( A = (0, 2) \).
2. Schlussfolgerung: Da keine offene Umgebung von \( y = 2 \) disjunkt zu \( A \) ist, folgt \( y = 2 \in \text{Cl}(A) \).

Damit ergibt sich, dass der Abschluss von \( A \) das abgeschlossene Intervall \( [0, 2] \) ist. Er enthält sowohl alle Punkte des offenen Intervalls als auch die beiden Randpunkte 0 und 2.

Wichtige Eigenschaften des Abschlusses

Der Abschluss spielt in der Topologie eine Schlüsselrolle. Seine Eigenschaften zeigen, wie eng er mit anderen Konzepten wie dem Inneren einer Menge oder abgeschlossenen Mengen verbunden ist.

• Inneres des Komplements und Komplement des Abschlusses
  Das Innere des Komplements einer Menge \( A \) ist identisch mit dem Komplement ihres Abschlusses: $$ \operatorname{Int}(X \setminus A) = X \setminus \operatorname{Cl}(A) $$
• Abschluss des Komplements und Komplement des Inneren
  Entsprechend gilt: $$ \operatorname{Cl}(X \setminus A) = X \setminus \operatorname{Int}(A) $$

Grundlegende Eigenschaften des Abschlussoperators

Die folgenden Eigenschaften des Abschlussoperators sind zentral für das Verständnis der topologischen Struktur eines Raums:

• Inklusion in abgeschlossene Mengen
  Ist \( C \) eine abgeschlossene Menge und \( A \subseteq C \), so gilt: $$ \text{Cl}(A) \subseteq C $$ Der Abschluss liegt also stets in jeder abgeschlossenen Menge, die \( A \) enthält. Das folgt direkt aus seiner Definition als kleinste abgeschlossene Menge, die \( A \) umfasst.
• Monotonie
  Für \( A \subseteq B \) gilt: $$ \text{Cl}(A) \subseteq \text{Cl}(B) $$ Der Abschlussoperator erhält Inklusionen - ein Ausdruck seiner monotonen Natur.
• Charakterisierung abgeschlossener Mengen
  Eine Menge \( A \) ist genau dann abgeschlossen, wenn gilt: $$ A = \text{Cl}(A) $$ Mit anderen Worten: Eine Menge ist abgeschlossen, wenn sie alle ihre Häufungspunkte enthält.
• Darstellung über Häufungspunkte
  Bezeichnet \( A' \) die Menge aller Häufungspunkte von \( A \), dann gilt: $$ \text{Cl}(A) = A \cup A' $$ Der Abschluss besteht also aus der ursprünglichen Menge und all ihren Häufungspunkten.
• Idempotenz
  Der Abschlussoperator ist idempotent: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ Eine erneute Abschlussbildung verändert die Menge nicht mehr.
• Inklusionseigenschaft
  Jede Menge ist stets in ihrem eigenen Abschluss enthalten: $$ A \subseteq \text{Cl}(A) $$

Der Begriff des Abschlusses ist damit weit mehr als eine technische Definition: Er beschreibt, wie sich Mengen im topologischen Raum „ausdehnen“, um ihre Umgebung vollständig einzuschließen. Ein Verständnis dieser Idee ist grundlegend, um zentrale Konzepte der modernen Topologie - etwa Stetigkeit, Konvergenz oder Kompaktheit - wirklich zu durchdringen.