Das Innere eines kartesischen Produkts

Seien $A$ und $B$ zwei Teilmengen, die jeweils in den topologischen Räumen $X$ und $Y$ liegen. Das Innere ihres kartesischen Produkts $A \times B$ ist identisch mit dem kartesischen Produkt ihrer jeweiligen Inneren. Es gilt also: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$

Diese Aussage ist ein grundlegendes Resultat der Produkttopologie und gilt insbesondere dann, wenn $A$ und $B$ offene Mengen in ihren jeweiligen topologischen Räumen sind.

Inhaltlich bedeutet der Satz Folgendes: Um das Innere eines kartesischen Produkts zu bestimmen, reicht es aus, zunächst die Inneren der einzelnen Mengen zu betrachten und diese anschließend miteinander zu kombinieren. Das Innere des Produkts entsteht also exakt aus den „inneren Teilen“ der Faktoren.

Ein konkretes Beispiel
Beweis

Ein konkretes Beispiel

Zur Veranschaulichung betrachten wir die topologischen Räume $X = \mathbb{R}$ und $Y = \mathbb{R}$ sowie die Teilmengen $A = (0, 2)$ und $B = (1, 3)$.

Beide Mengen sind offene Intervalle der reellen Zahlengeraden $\mathbb{R}$.

Bestimmen wir zunächst ihre Inneren.

Da $A$ offen ist, stimmt sein Inneres mit der Menge selbst überein:

$$ \text{Int}(A) = (0, 2) $$

Entsprechend gilt für $B$:

$$ \text{Int}(B) = (1, 3) $$

Betrachten wir nun das Produkt der Inneren:

$$ \text{Int}(A) \times \text{Int}(B) = (0, 2) \times (1, 3) $$

Diese Menge besteht aus allen geordneten Paaren $(x, y)$, bei denen $x$ zwischen 0 und 2 und $y$ zwischen 1 und 3 liegt:

$$ \text{Int}(A) \times \text{Int}(B) = \{(x, y) \mid x \in (0, 2),\ y \in (1, 3)\} $$

Geometrisch entspricht diese Menge einem offenen Rechteck in der Ebene $\mathbb{R}^2$. Die Randlinien gehören nicht dazu.

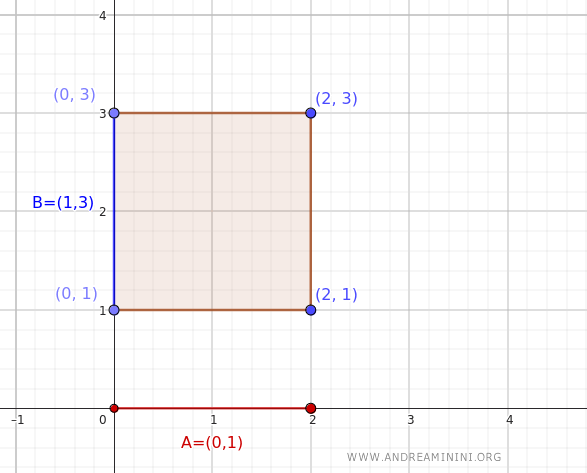
Offenes Rechteck in der Ebene R^2 als kartesisches Produkt zweier offener Intervalle

Bestimmen wir nun das Innere des kartesischen Produkts $A \times B = (0, 2) \times (1, 3)$:

Auch hier erhalten wir genau dasselbe offene Rechteck in $\mathbb{R}^2$.

Damit bestätigt dieses Beispiel unmittelbar die Aussage des Satzes:

$$ \text{Int}(A \times B) = (0, 2) \times (1, 3) = \text{Int}(A) \times \text{Int}(B) $$

Das Resultat zeigt anschaulich, dass sich das Innere eines Produkts vollständig aus den Inneren seiner Faktoren zusammensetzt.

Beweis

Der Beweis basiert auf dem Nachweis zweier Inklusionen. Zunächst zeigen wir, dass das Produkt der Inneren im Inneren des Produkts enthalten ist. Anschließend weisen wir die umgekehrte Inklusion nach. Zusammen ergeben diese beiden Schritte die gewünschte Gleichheit.

1] Das Produkt der Inneren ist im Inneren des Produkts enthalten

Zu zeigen ist:

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

Sei dazu $(x, y)$ ein Punkt mit $x \in \text{Int}(A)$ und $y \in \text{Int}(B)$.

Da $x$ ein innerer Punkt von $A$ ist, existiert eine offene Menge $U \subseteq X$ mit $x \in U \subseteq A$.

Analog existiert eine offene Menge $V \subseteq Y$ mit $y \in V \subseteq B$.

Das kartesische Produkt $U \times V$ ist eine offene Menge im Produktraum $X \times Y$, enthält den Punkt $(x, y)$ und liegt vollständig in $A \times B$.

Damit ist $(x, y)$ ein innerer Punkt von $A \times B$, und die Inklusion ist gezeigt:

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

2] Das Innere des Produkts ist im Produkt der Inneren enthalten

Nun zeigen wir die umgekehrte Inklusion:

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$

Sei $(x, y) \in \text{Int}(A \times B)$. Dann existiert per Definition des Inneren eine offene Menge $W \subseteq X \times Y$ mit $(x, y) \in W \subseteq A \times B$.

Da die Produkttopologie eine Basis aus Mengen der Form $U \times V$ besitzt, finden wir offene Mengen $U \subseteq X$ und $V \subseteq Y$ mit

$$ (x, y) \in U \times V \subseteq W. $$

Aus der Inklusion $U \times V \subseteq A \times B$ folgt unmittelbar $U \subseteq A$ und $V \subseteq B$.

Damit ist $x \in \text{Int}(A)$ und $y \in \text{Int}(B)$, also

$$ (x, y) \in \text{Int}(A) \times \text{Int}(B). $$

Damit ist auch die zweite Inklusion bewiesen:

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$

3] Schlussfolgerung

Da beide Inklusionen gelten, nämlich

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

und

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B), $$

folgt insgesamt die Gleichheit

$$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B). $$

Damit ist der Satz bewiesen.