Satz über die Charakterisierung des Randes
Ein Punkt \( x \) gehört genau dann zum Rand einer Menge \( A \), wenn jede seiner Umgebungen sowohl Punkte aus \( A \) als auch Punkte aus dem Komplement \( X - A \) enthält.
Das bedeutet: Keine Umgebung von \( x \) liegt vollständig in \( A \) und ebenso wenig vollständig außerhalb von \( A \). Genau diese doppelte Berührung macht Randpunkte topologisch relevant.
Ein einfaches und anschauliches Beispiel
Betrachten wir das offene Intervall \( A = (0, 1) \subset \mathbb{R} \). Dieses Beispiel eignet sich hervorragend, um die Definition intuitiv zu verstehen.
Die Punkte 0 und 1 liegen auf dem Rand des Intervalls. Jede beliebig kleine Umgebung dieser Punkte enthält gleichzeitig Punkte im Inneren des Intervalls und Punkte außerhalb davon.
- Der Punkt 1
Eine Umgebung wie \( (1 - \epsilon, 1 + \epsilon) \) enthält immer einen Abschnitt innerhalb von \( A \) und zugleich einen Abschnitt außerhalb. Damit ist 1 ein typischer Randpunkt.
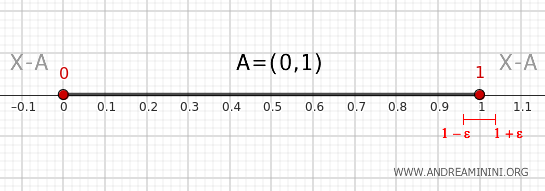
- Der Punkt 0
Auch 0 erfüllt genau dieselbe Bedingung: Jede Umgebung von 0 schneidet sowohl das Intervall als auch dessen Komplement. Deshalb gehört 0 ebenfalls zum Rand.
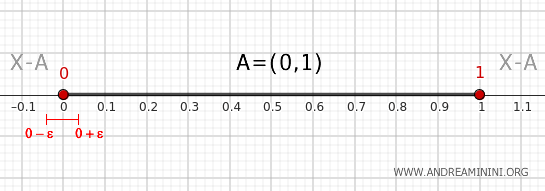
- Punkte im Inneren
Jeder Punkt \( x \) mit \( 0 < x < 1 \) besitzt eine Umgebung, die vollständig in \( A \) liegt. Diese Umgebung berührt das Komplement nicht, weshalb solche Punkte nicht zum Rand gehören.
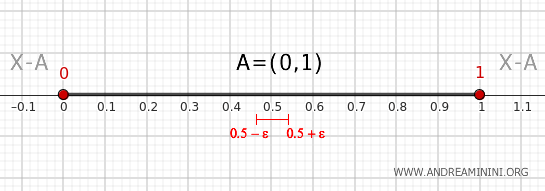
- Punkte außerhalb
Für Punkte außerhalb des Intervalls, abgesehen von den Endpunkten 0 und 1, existieren Umgebungen, die vollständig im Komplement \( X - A \) liegen. Solche Punkte schneiden das Intervall nicht und gehören daher nicht zum Rand.
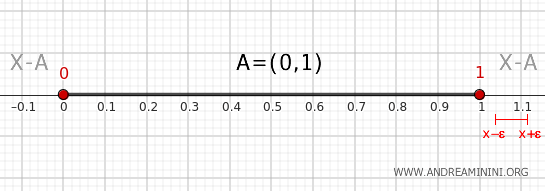
Aus diesen Beobachtungen folgt ohne weiteres:
$$ \partial A = \{0, 1\} $$
Ein Punkt liegt genau dann im Rand, wenn keine seiner Umgebungen vollständig im Inneren der Menge oder vollständig im Komplement liegt. Dieses Kriterium ist eine der grundlegenden Charakterisierungen des topologischen Randbegriffs.
Der Beweis des Satzes
Die Aussage lässt sich durch zwei äquivalente Bedingungen präzise begründen.
1] Angenommen \( x \in \partial A \)
Dann gilt per Definition:
$$ x \in \text{Cl}(A) \quad \text{und} \quad x \notin \text{Int}(A) $$
Dass \( x \) in der abgeschlossenen Hülle liegt, bedeutet, dass jede Umgebung von \( x \) Punkte aus \( A \) enthält.
Dass \( x \) nicht im Inneren liegt, bedeutet, dass keine Umgebung vollständig in \( A \) enthalten ist. Jede Umgebung enthält daher auch Punkte aus dem Komplement.
Damit schneidet jede Umgebung sowohl \( A \) als auch \( X - A \).
2] Angenommen jede Umgebung von \( x \) schneidet sowohl \( A \) als auch dessen Komplement
Dann folgt sofort:
$$ x \in \text{Cl}(A) \quad \text{und} \quad x \in \text{Cl}(X - A) $$
Da für Mengen gilt:
$$ \text{Cl}(X - A) = X - \text{Int}(A) $$
ergibt sich:
$$ x \notin \text{Int}(A) $$
Und damit:
$$ x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A $$
Damit ist die Äquivalenz vollständig gezeigt und der Satz über die Charakterisierung des Randes präzise bewiesen.