Différence entre égalité et congruence

En géométrie, on rencontre souvent les notions d’égalité et de congruence. Elles paraissent proches, mais elles désignent en réalité deux idées différentes. Les distinguer permet de mieux comprendre comment on compare des figures dans un espace géométrique.

• Égalité
  

  Deux figures sont égales lorsqu’elles coïncident exactement point par point, sans qu’il soit nécessaire de les déplacer ou de les transformer.

  Autrement dit, si deux figures sont égales, elles se superposent parfaitement. Même forme, mêmes dimensions, même position. En géométrie, on écrit simplement : $$ A = B $$

  Un cas classique se trouve dans le triangle isocèle. La hauteur issue du sommet principal et la médiane correspondante sont en fait le même segment, ce qui les rend égales. Voici une illustration d’un cas d’égalité entre deux figures :
  

• Congruence
  

  Deux figures sont congruentes si l’on peut les superposer exactement après une transformation rigide, comme une rotation, une translation ou une réflexion.

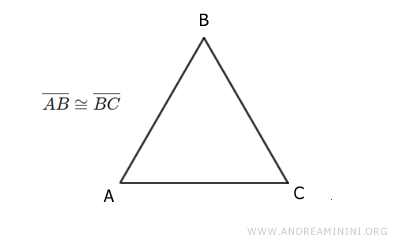
  Les figures congruentes partagent la même forme et les mêmes dimensions, mais pas forcément la même position dans l’espace. Pour exprimer cette relation, on utilise le symbole ≅ $$ A \cong B $$

  Dans un triangle isocèle, par exemple, les côtés AB et BC sont congruents. Une simple rotation suivie d’une translation suffit à les placer l’un sur l’autre. Voici une représentation claire de cette situation :
  

On peut retenir l’idée suivante : l’égalité est un cas particulier de la congruence. Deux figures égales sont toujours congruentes, mais deux figures congruentes ne sont pas forcément égales, car elles peuvent occuper des positions différentes.

Dans tous les cas, la forme et les dimensions restent identiques. Ce qui change, c’est uniquement leur emplacement dans l’espace.

Et ainsi de suite.