Les postulats d’Euclide

Dans son ouvrage majeur « Les Éléments », Euclide présente cinq postulats qui forment le socle de la géométrie euclidienne. Ces principes simples ont structuré pendant des siècles notre manière de comprendre l’espace.

Ces énoncés, acceptés sans démonstration, servent de points de départ à toute la géométrie plane, telle qu’elle est enseignée aujourd’hui dans les programmes scolaires.

Remarque: Modifier ne serait-ce qu’un seul de ces postulats suffit à créer une géométrie entièrement différente, appelée géométrie non euclidienne.

Voici les cinq postulats tels qu’ils sont traditionnellement présentés.

Premier postulat

Par deux points distincts, il existe toujours une seule droite qui les relie.

Ce principe établit à la fois l’existence d’une droite passant par deux points et son caractère unique. Tout découle de cette idée simple.

Corollaires

De ce postulat, on tire plusieurs conséquences immédiates:

• Par un point donné, on peut tracer une infinité de droites.
• Toute droite contient au moins deux points.
• Trois points non alignés déterminent un unique plan.
• Trois points alignés déterminent une seule droite.
• Une droite peut appartenir à une infinité de plans.

Deuxième postulat

Un segment peut être prolongé indéfiniment pour former une droite complète.

Troisième postulat

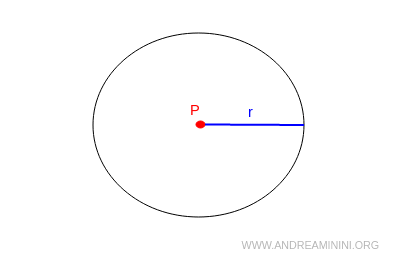
À partir d’un point donné et d’un segment de longueur fixée, on peut tracer un cercle ayant ce point pour centre et ce segment pour rayon.

Quatrième postulat

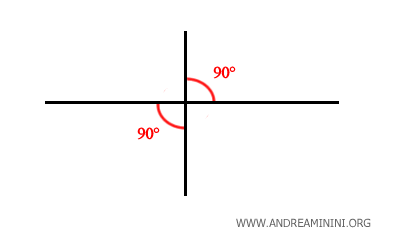
Tous les angles droits possèdent la même mesure. Ils sont donc congruents.

Cinquième postulat

Si une droite « r » coupe deux droites « s » et « t » de façon que la somme des angles intérieurs α et β situés du même côté de « r » soit inférieure à deux angles droits (α + β < 180°), alors les droites « s » et « t », prolongées indéfiniment, se rencontreront en un point P.

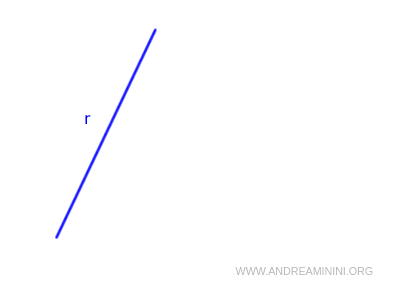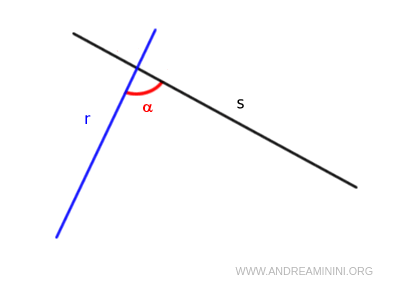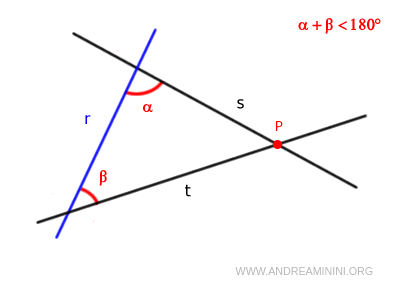
Ce postulat est connu sous le nom de postulat des parallèles. Il permet de définir précisément ce que l’on entend par deux droites parallèles: si la somme des angles intérieurs vaut exactement 180°, les droites ne se rencontreront jamais dans le plan.

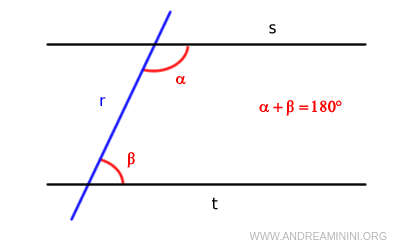
Au fil des siècles, ce cinquième postulat a été reformulé de nombreuses manières équivalentes, devenant l’un des sujets les plus débattus de l’histoire des mathématiques.

Remarque: Pendant plus de deux mille ans, les mathématiciens ont tenté de démontrer ce postulat à partir des quatre premiers, sans succès. Le XIXe siècle a finalement montré qu’une telle démonstration était impossible. En modifiant ce postulat, on ouvre la voie aux géométries non euclidiennes, parmi lesquelles la géométrie sphérique, hyperbolique et elliptique.

Et ainsi de suite.