La congruence en géométrie
Deux figures géométriques sont dites congruentes lorsqu’on peut les faire coïncider point par point au moyen d’un mouvement rigide. Autrement dit, elles ont exactement la même forme et les mêmes dimensions.
Les mouvements rigides, aussi appelés isométries, sont des transformations qui préservent les distances et les angles. Il peut s’agir d’une translation, d’une rotation ou d’une symétrie. Ces transformations permettent de déplacer une figure sans la déformer.
C’est pourquoi deux figures congruentes peuvent être orientées différemment ou situées à des endroits distincts, tout en restant essentiellement la même figure.
La congruence se note avec le symbole ≅, qui indique une égalité « à position près ».
$$ A ≅ B $$
Cette notion est centrale en géométrie euclidienne. Elle sert à comprendre quand deux figures possèdent la même structure, indépendamment de leur emplacement.
Note. Une isométrie modifie seulement la position d’une figure, jamais sa forme ni sa taille. Si une figure peut être obtenue à partir d’une autre par une suite d’isométries, alors elles sont congruentes. C’est l’un des piliers de la géométrie classique.
Exemple à partir d’un triangle
Voici deux copies d’un même triangle. L’une semble simplement renversée par rapport à l’autre.
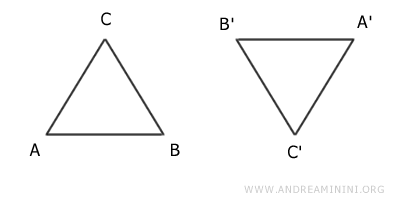
À première vue, ils ne sont pas identiques, car leurs positions diffèrent. Pourtant, ils sont congruents. Une rotation suivie d’une translation suffit à les superposer parfaitement.
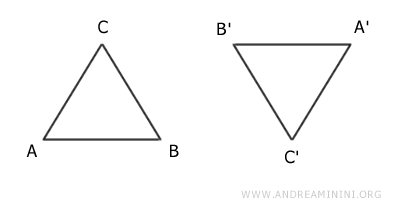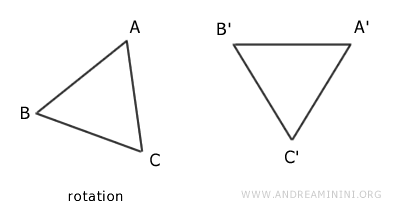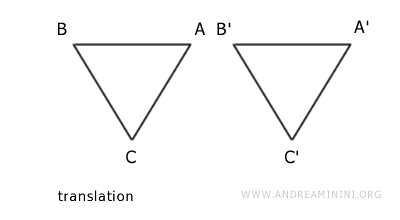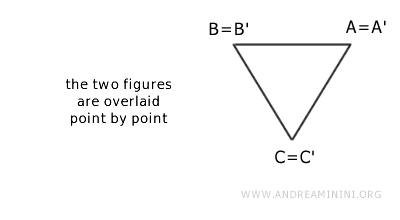
Une fois déplacés correctement, les deux triangles coïncident point par point.
Autres exemples simples de congruence
En géométrie plane :
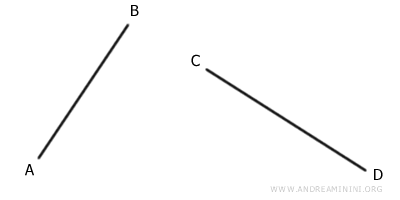
- Deux segments sont congruents lorsqu’ils ont la même longueur, comme AB ≅ CD.
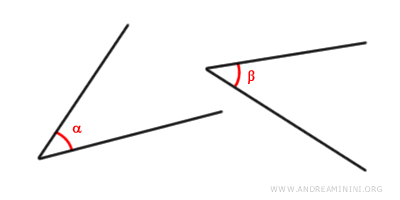
- Deux angles sont congruents lorsqu’ils ont la même mesure. On écrit alors α ≅ β.
- Deux polygones sont congruents si leurs côtés et leurs angles correspondants sont congruents.
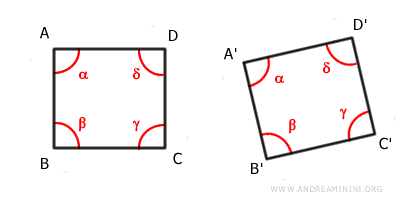
Note. Ces observations conduisent à des résultats fondamentaux en géométrie euclidienne : toutes les droites sont congruentes entre elles, tous les rayons sont congruents, et tous les demi-plans le sont également.
Comment démontrer que deux triangles sont congruents
Pour les triangles, la congruence repose sur trois critères bien établis. Il suffit qu’un seul soit vérifié pour conclure que deux triangles sont congruents :
- Côté-Côté-Côté (CCC). Les trois côtés correspondants ont la même longueur.
- Côté-Angle-Côté (CAC). Deux côtés correspondants et l’angle compris sont congruents.
- Angle-Côté-Angle (ACA). Deux angles correspondants et le côté compris sont congruents.
Note. Ces critères sont équivalents. Dès qu’un triangle vérifie l’un d’eux, il vérifie automatiquement les autres.
Congruence ou égalité ?
La distinction est importante.
Deux figures sont égales lorsqu’elles coïncident point par point sans qu’aucune transformation ne soit nécessaire. Elles ont la même forme, les mêmes dimensions et la même position.
L’égalité se note simplement :
$$ A = B $$
Dans un triangle isocèle, la hauteur et la médiane issues du sommet principal sont égales, car elles se confondent exactement.
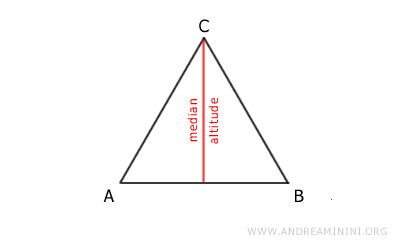
La congruence, elle, permet une coïncidence après déplacement rigide. Deux figures congruentes peuvent donc être orientées ou placées différemment, tout en ayant la même structure.
On écrit :
$$ A ≅ B $$
Par exemple, dans un triangle isocèle, les côtés AB et BC sont congruents. Une rotation et une translation permettent de les faire coïncider.

Retenons que l’égalité est une notion plus restrictive, alors que la congruence accepte la possibilité d’un déplacement.
Différence entre congruence et similitude
Deux figures semblables ont la même forme, mais pas nécessairement les mêmes dimensions. Elles sont proportionnelles, mais pas superposables.
C’est le cas des triangles ci-dessous : ils ne sont pas congruents, mais ils sont semblables.

Ils ont la même structure géométrique, mais le premier est simplement une version agrandie du second.
Les propriétés fondamentales de la congruence
La congruence forme une relation d’équivalence sur l’ensemble des figures géométriques. Elle vérifie trois propriétés essentielles :
- Réflexivité. Toute figure est congruente à elle-même.
- Symétrie. Si A est congruente à B, alors B est congruente à A.
- Transitivité. Si A est congruente à B et B à C, alors A est congruente à C.
Autrement dit, la congruence classe les figures en familles qui partagent la même structure métrique. Cette idée est au cœur de la géométrie euclidienne.