Lieu géométrique
Un lieu géométrique est l'ensemble des points d'un espace qui partagent la même propriété ou la même condition. C'est un outil simple et puissant pour comprendre comment se forment de nombreuses figures en géométrie.
La propriété qui définit cet ensemble s'appelle sa propriété caractéristique. Lorsqu'elle est exprimée à l'aide d'une équation, on parle alors d'équation du lieu.
Décrire un lieu géométrique revient donc à montrer que tous ses points vérifient la même condition et qu'aucun point extérieur ne la satisfait. C'est cette précision qui permet de relier les figures dessinées à leurs équations.
Pourquoi c'est important : Les lieux géométriques sont au cœur de la géométrie analytique. Ils permettent de passer du dessin à l'équation et de comprendre, de manière unifiée, des courbes, des segments ou des surfaces.
Un premier exemple
Considérons une droite. On peut la voir comme l'ensemble des points du plan qui respectent une relation linéaire entre x et y, autrement dit une condition d'alignement.
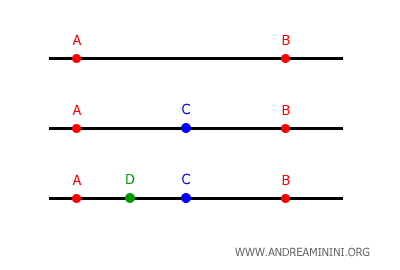
Pour savoir si un point appartient à cette droite, il suffit de vérifier qu'il respecte l'équation suivante :
$$ ax + by + c = 0 $$
Cette équation n'est rien d'autre que l'équation du lieu.
Un exemple plus riche : la médiatrice d'un segment
La médiatrice d'un segment est l'ensemble des points du plan qui sont à égale distance des deux extrémités A et B.
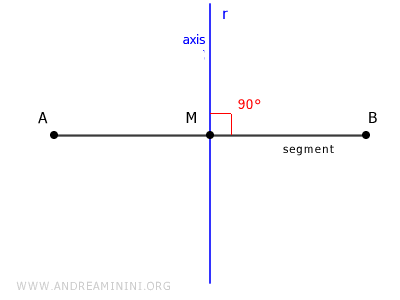
Sa propriété caractéristique est simple : $ \overline{PA} = \overline{PB} $. Cela signifie que la médiatrice passe par le milieu du segment AB et qu'elle est perpendiculaire au segment.
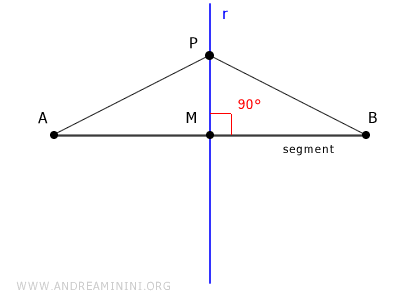
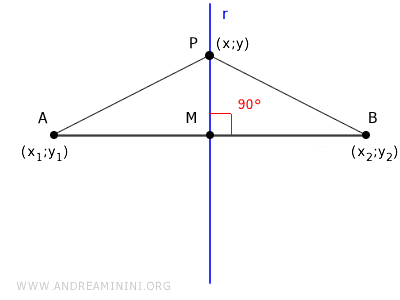
Pour exprimer cette idée à l'aide d'une équation, on calcule les distances AP et BP d'un point P(x, y) aux deux extrémités :
$ \underbrace{\sqrt{(y - y_1)^2 + (x - x_1)^2}}_{AP} = \underbrace{\sqrt{(y - y_2)^2 + (x - x_2)^2}}_{BP} $
Cette égalité décrit précisément tous les points de la médiatrice.
Que se passe-t-il dans le calcul : Pour établir cette expression, on applique le théorème de Pythagore dans les triangles AMP et BMP. Les longueurs AM, BM et MP permettent d'exprimer AP et BP de manière entièrement algébrique. On obtient ainsi l'équation :
$$ \underbrace{\sqrt{(y - y_1)^2 + (x - x_1)^2}}_{AP} = \underbrace{\sqrt{(y - y_2)^2 + (x - x_2)^2}}_{BP} $$
D'autres lieux géométriques incontournables
- Le cercle, défini par tous les points situés à distance constante d'un centre.
- La bissectrice d'un angle, qui regroupe les points équidistants des deux côtés de l'angle.
- La parabole, ensemble des points équidistants d'un foyer et d'une directrice.
- L'ellipse, ensemble des points dont la somme des distances à deux foyers reste constante.
- L'hyperbole, définie par une différence de distances constante aux deux foyers.
Ces exemples montrent comment une idée géométrique simple peut être exprimée de façon précise grâce à une équation. C'est tout l'intérêt des lieux géométriques.