Entités géométriques

Les entités géométriques sont les éléments de base qui permettent de comprendre, décrire et analyser l’espace. Elles servent à structurer les formes, les objets et leurs relations dans l’étude de la géométrie.

Chaque entité possède un nom précis et se définit par un ensemble de propriétés qui la distinguent des autres.

Exemple: Un carré est une figure plane composée de quatre côtés de même longueur et de quatre angles droits.

Pour décrire un objet géométrique de manière rigoureuse, on s’appuie sur un vocabulaire spécialisé. Chaque terme utilisé doit lui-même être clairement défini.

Exemple: Dans la définition du carré apparaissent les notions de « côté » et d’« angle », qui nécessitent elles aussi une définition précise.

Certaines entités géométriques primitives, en revanche, sont acceptées sans définition formelle. Elles constituent le point de départ de toute construction géométrique.

Les principales entités primitives sont les suivantes:

• Points
  Le point est une entité sans dimensions. Il ne possède ni longueur, ni largeur, ni épaisseur. On le représente par un simple signe graphique et il sert à indiquer une position dans l’espace. Par convention, les points sont désignés par des lettres majuscules (A, B, C, etc.).
  
• Droites
  La droite est un alignement infini de points qui s’étend sans limite dans les deux directions. Elle possède une longueur, mais aucune largeur ni épaisseur. Dans les schémas, on la désigne généralement à l’aide de lettres minuscules (r, s, t, etc.).
  
• Plans
  Le plan est une surface bidimensionnelle qui s’étend indéfiniment en longueur et en largeur, sans épaisseur. Il sert de cadre pour l’étude des figures géométriques planes.
  

À partir de ces entités primitives, on peut définir toutes les autres formes et figures géométriques.

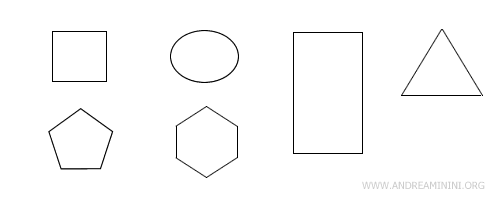
• Figures planes, comme les cercles ou les carrés. Elles se situent dans un plan et possèdent une aire mais aucun volume.
  
• Solides géométriques, comme les sphères ou les cubes. Ce sont des objets tridimensionnels qui possèdent un volume mesurable.
  

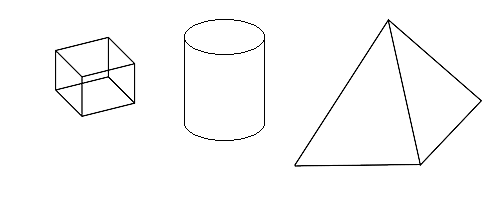
Cette base conceptuelle permet ensuite d’explorer progressivement l’ensemble des notions étudiées en géométrie.