Point

En géométrie euclidienne, le point est l'une des notions de base qui permettent de définir les droites, les plans et, plus largement, toute la structure géométrique.

On parle de notion primitive, parce qu'un point ne se définit pas à partir d'autres objets. Toute théorie géométrique repose sur quelques concepts acceptés tels quels, et le point fait partie de ces éléments fondamentaux.

Intuitivement, un point est un objet sans dimension. Il n'a ni longueur, ni largeur, ni hauteur. Il ne possède aucune forme et ne peut pas être décomposé. Euclide le décrivait comme « ce qui n'a pas de parties », une formule encore reprise aujourd'hui.

Pour le représenter sur une figure, on trace une petite marque. Ce n'est qu'un repère visuel, indispensable pour travailler sur un dessin, mais qui ne doit pas être confondu avec le point géométrique lui-même.

Le signe tracé sur le papier occupe inévitablement un espace. En réalité, le point géométrique est entièrement adimensionnel. Toute représentation graphique sert seulement à matérialiser une idée qui, elle, demeure abstraite.

Dans les textes de géométrie, les points sont nommés à l'aide de lettres majuscules, comme \( A \), \( B \) ou \( C \). Cette notation permet de désigner sans ambiguïté une position précise dans l'espace.

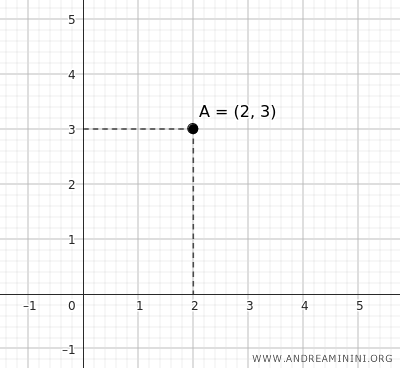
Sur un plan cartésien, un point est décrit par un couple de coordonnées \((x, y)\). Ce simple duo de valeurs suffit à le situer exactement.

Par exemple, le point \( A = (2, 3) \) se trouve à 2 unités le long de l'axe des abscisses et à 3 unités le long de l'axe des ordonnées.

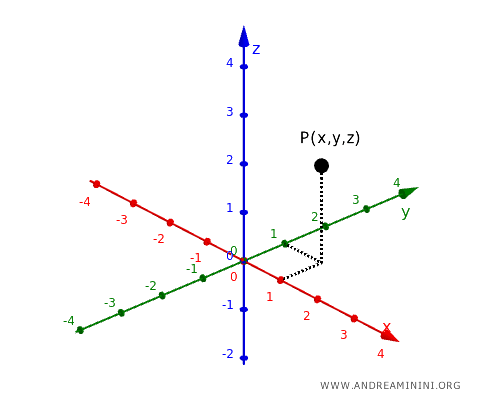
Dans l'espace tridimensionnel, un point est repéré par trois coordonnées \((x, y, z)\). Chacune indique sa distance par rapport à l'un des trois plans de référence.

À partir de cette idée simple, on construit l'essentiel de la géométrie.

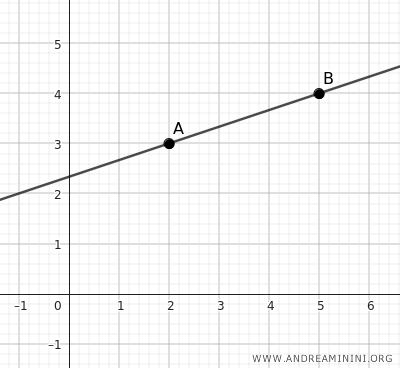
Une droite, par exemple, est entièrement déterminée par deux points distincts. On peut la voir comme une succession infinie de points alignés.

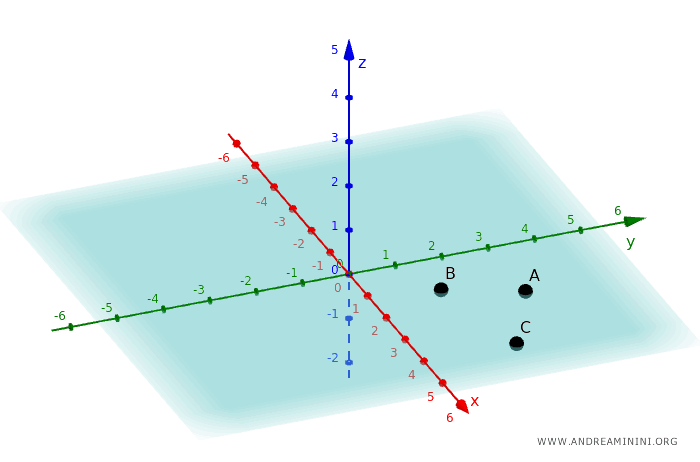
Un plan, de son côté, est défini par trois points non alignés. Il s'agit d'une surface plane à deux dimensions, constituée elle aussi d'une infinité de points.

Segments, angles, polygones et autres figures géométriques prennent tous naissance à partir des points. C'est à partir de cette notion première que se structure l'ensemble de la géométrie euclidienne.