Jednostavno povezani prostori u topologiji
Topološki prostor naziva se jednostavno povezan ako se svaka zatvorena putanja u njemu može neprekidno smanjiti i svesti u jednu tačku, bez napuštanja prostora.
Drugim riječima, u jednostavno povezanom prostoru svaka petlja može se „zategnuti" do tačke, bez prekidanja ili izlaska iz prostora. Takav prostor je kompaktan, bez unutrašnjih rupa ili praznina koje bi sprječavale tu deformaciju.
To znači da prostor predstavlja jednu cjelovitu strukturu - povezan je i bez „praznih mjesta" unutar sebe.
Napomena: svaki jednostavno povezan prostor je i povezan prostor. Međutim, obrnuto ne mora biti tačno: povezan prostor ne mora uvijek biti jednostavno povezan.
Primjer iz svakodnevne topologije
Zamislite sferu. To je tipičan primjer jednostavno povezanog prostora: svaka zatvorena linija povučena po njenoj površini može se polako skupiti u jednu tačku, bez napuštanja sfere.
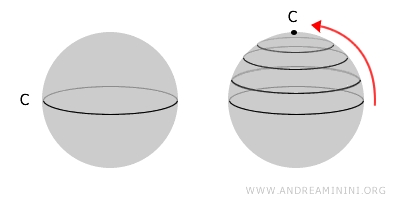
S druge strane, torus - poznat i kao „krofna" - nije jednostavno povezan prostor. Njegova centralna rupa onemogućava da se određene petlje kontrahuju do tačke, jer bi to zahtijevalo prolazak kroz „rupu" koja ne pripada prostoru.
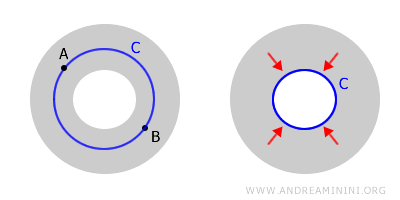
Ovaj primjer jasno pokazuje da povezanost ne znači uvijek i jednostavnu povezanost. „Krofna" je povezana jer se bilo koje dvije tačke na njenoj površini mogu spojiti putem koji u potpunosti ostaje unutar prostora. Ali nije jednostavno povezana, jer se ne mogu sve zatvorene krive na njoj svesti u tačku.
Kada je prostor povezan, ali ne i jednostavno povezan, kažemo da je višestruko povezan. Tipični primjeri su prstenasti regioni i toroidalni prostori.
Zaključak: jednostavna povezanost je stroži uslov od same povezanosti putem lukova. Ona zahtijeva ne samo da se tačke mogu međusobno povezati, već i da se svaka zatvorena putanja može neprekidno „ugasiti" unutar prostora.