Povezani prostori i clopen skupovi: kako prepoznati topološku povezanost
Topološki prostor \( X \) naziva se povezanim ako i samo ako su jedini njegovi podskupovi koji su istovremeno otvoreni i zatvoreni (tzv. clopen skupovi) cijeli prostor \( X \) i prazan skup \( \emptyset \).
Drugim riječima, prostor je povezan kada ga nije moguće razložiti na dva odvojena i neprazna otvorena dijela. Ako su jedini clopen skupovi koje sadrži cijeli prostor i prazan skup, tada u njemu ne postoji topološko razdvajanje.
Ovaj teorem pruža jednostavan, ali snažan kriterij za topološku povezanost. Omogućuje nam da utvrdimo je li prostor povezan bez oslanjanja na složenije pojmove poput povezanosti putem putanja.
Kako to razumjeti
U topologiji, podskup koji je istovremeno otvoren i zatvoren zapravo razdvaja prostor. Na taj način prostor \( X \) postaje sastavljen od dva disjunktna i neprazna otvorena dijela.
Ako takav skup postoji, kažemo da je prostor nepovezan (ili diskonektan). Ako ne postoji, prostor ostaje povezan jer ne može biti podijeljen na odvojene dijelove.
Napomena: u svakom topološkom prostoru cijeli prostor \( X \) i prazan skup \( \emptyset \) uvijek su i otvoreni i zatvoreni. To su tzv. trivijalni clopen skupovi.
Primjer 1: konačan nepovezan prostor
Razmotrimo \( X = \{ a, b, c, d \} \) s topologijom \( T \) definiranom otvorenim skupovima \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).
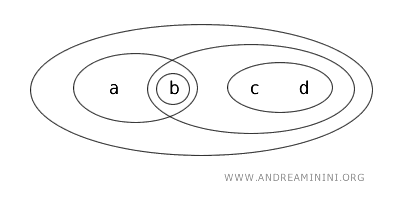
U ovom primjeru, podskup \( \{ a, b \} \) je clopen jer:
- je otvoren, budući da pripada kolekciji otvorenih skupova topologije \( T \);
- je zatvoren, jer je njegov komplement \( X \setminus \{ a, b \} = \{ c, d \} \) također otvoren u \( T \).
Iz toga zaključujemo da je prostor \( (X, T) \) nepovezan, jer sadrži pravi neprazan podskup koji je clopen. Dovoljno je postojanje samo jednog takvog skupa da prostor ne bude povezan.
Drugim riječima, prostor se može prikazati kao unija dva disjunktna otvorena skupa, \( \{ a, b \} \) i \( \{ c, d \} \), što znači da uvjet topološke povezanosti nije ispunjen.
Primjer 2: realna prava
Uzmimo skup realnih brojeva \( \mathbb{R} \) sa standardnom topologijom koju čine svi otvoreni intervali \( (a, b) \).
U toj topologiji, intervali \( (a, b) \) su otvoreni, ali nisu zatvoreni, dok su \( [a, b] \) zatvoreni, ali nisu otvoreni. Jedini skupovi u \( \mathbb{R} \) koji su i otvoreni i zatvoreni jesu cijela prava \( \mathbb{R} \) i prazan skup \( \emptyset \).
Prema tome, realna prava s ovom topologijom je povezan prostor. Ne može se razdvojiti na dva odvojena otvorena dijela bez narušavanja njene cjelovitosti.
Primjer 3: nepovezan podprostor realne prave
Razmotrimo podprostor \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) s induciranom topologijom koja dolazi iz standardne topologije na \( \mathbb{R} \).
U ovom slučaju, intervali \( (0,1) \) i \( (2,3) \) su i otvoreni i zatvoreni u \( X \), jer je komplement svakog od njih u \( X \) upravo drugi interval:
- komplement skupa \( (0,1) \) u \( X \) je \( (2,3) \), koji je otvoren u \( X \);
- komplement skupa \( (2,3) \) u \( X \) je \( (0,1) \), koji je također otvoren u \( X \).
Ova dva podskupa su, dakle, clopen. To znači da prostor \( X \) nije povezan jer se sastoji od dvije odvojene povezane komponente: \( (0,1) \) i \( (2,3) \). Nemoguće je kontinuirano povezati točke iz jednog intervala s točkama iz drugog, što jasno pokazuje da prostor nije povezan.