Prostori povezani lukovima

Kažemo da je topološki prostor S povezan lukovima ako za svake dve tačke A i B u tom prostoru postoji neprekidan put koji ih spaja, a da se pritom ne izlazi iz prostora.

Zamislite običan list papira, bez ivica i granica.

Taj list predstavlja otvorenu, neprekinutu površinu. Na njemu možete povući olovkom liniju koja spaja bilo koje dve tačke A i B, bez podizanja olovke sa papira.

Drugim riječima, put koji povlačimo nikada ne napušta prostor u kojem se nalaze tačke A i B.

Svaki prostor povezan lukovima ujedno je i povezan prostor.

To ima smisla: ako bi prostor bio razdvojen, sastojao bi se od više odvojenih dijelova, pa ne bi bilo moguće spojiti dvije tačke neprekidnom linijom unutar njega.

Ali obrnuto ne vrijedi uvijek. Ne mora svaki povezan prostor biti i povezan lukovima.

Pogledajmo jedan zanimljiv primjer koji na prvi pogled djeluje paradoksalno, ali je sasvim ispravan.

Razmotrimo dva skupa, Q i T:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

Skup Q sadrži sve tačke na sinusoidnoj krivoj definisanoj za sve realne brojeve osim nule, gdje funkcija nije definisana jer bi došlo do dijeljenja nulom.

Skup T je jednostavan - sastoji se samo od tačke nula.

Iako su odvojeni, skupovi Q i T su beskrajno blizu jedan drugom. To se jasno vidi na grafikonu funkcije sin(1/x).

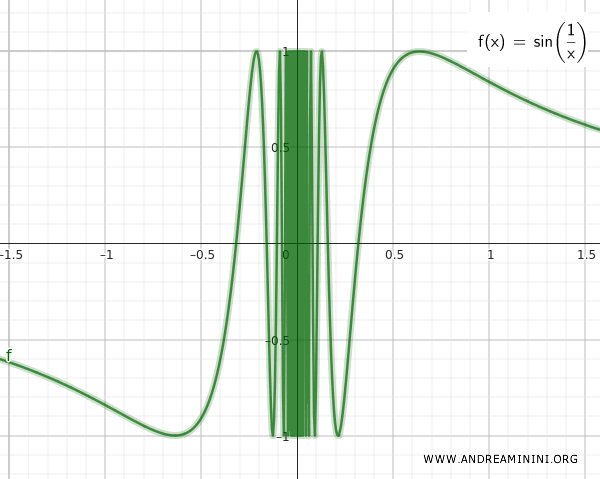
Ako ih spojimo, dobijamo skup S:

$$ S = Q \cup T $$

Skup S jeste povezan, jer za svako ε>0 postoji okolina oko nule (0-ε, 0+ε) koja sadrži tačke iz skupa Q.

Drugim riječima, nula je tačka nakupljanja funkcije sin(1/x).

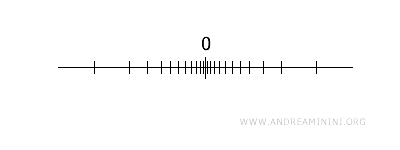
Ipak, S nije povezan lukovima jer ne postoji nijedan neprekidan put koji bi spojio neku tačku iz Q sa tačkom nula.

Napomena: Kod funkcije f(x)=1/x situacija je drugačija. Tu su skupovi Q i T jasno odvojeni i nisu beskrajno bliski.

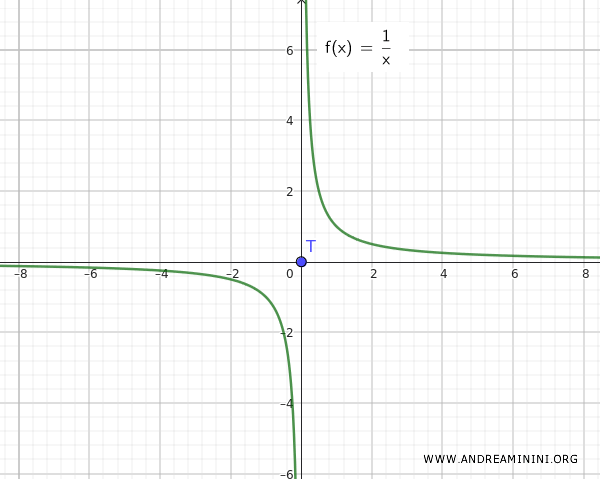
Ovaj primjer pokazuje da unija povezanog skupa Q={∀ x ∈ R-{0}, 1/x} i izolovane tačke T={0} ne mora biti povezan prostor, osim ako ta tačka (nula) nije i tačka nakupljanja.

 I tako dalje.