Povezanost u topologiji

U topologiji kažemo da je prostor povezan ako ga nije moguće razdvojiti na dva odvojena otvorena skupa. Drugim riječima, povezanost opisuje koliko je neki prostor "cjelovit" - da li se svaka dvije tačke mogu spojiti neprekidnim putem koji ostaje unutar tog prostora.

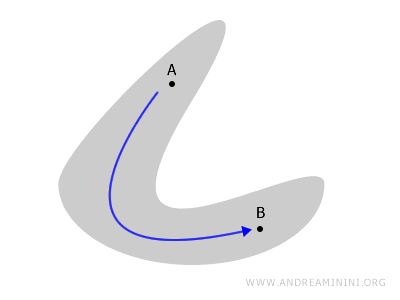
Povezanost nam govori kako su dijelovi jednog topološkog prostora međusobno povezani, odnosno gdje se taj prostor prekida ili razdvaja.

Ovaj pojam je jedan od temeljnih u topologiji, zajedno s pojmom kontinuiteta, jer pomaže matematičarima da razumiju "strukturu" prostora iznutra.

Povezanost se koristi u mnogim područjima matematike - od analize do geometrije - jer otkriva kako su različiti dijelovi prostora povezani i kako međusobno djeluju. Ona pomaže u klasifikaciji i razumijevanju različitih tipova prostora.

Primjer iz prakse

Zamislite ravnu figuru ili trodimenzionalno tijelo. Takav prostor se smatra povezanim ako za svake dvije tačke A i B postoji neprekidan put koji ih spaja, a da pri tom ne izlazi iz prostora.

Ako, međutim, neki dijelovi prostora nisu međusobno dodirnuti, govorimo o nepovezanom prostoru.

Na primjer, ako je prostor podijeljen na dva dijela, svaki pokušaj da se tačke A i B povežu zahtijevao bi da "izađemo" iz prostora.

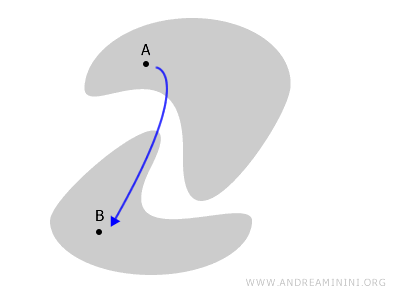
Drugim riječima, prostor više nije cjelina - on se "raspao" na dva odvojena dijela.

Kada je prostor nepovezan?

Zamislite dvije sobe u istoj zgradi, razdvojene zidom. Svaka soba je otvoren prostor, ali zid između njih onemogućava prelazak iz jedne u drugu bez izlaska iz prostora.

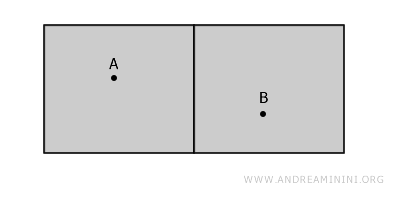
Iako se te sobe nalaze jedna pored druge, one nisu povezane - svaki put od tačke A do tačke B morao bi proći kroz zid, koji ne pripada prostoru.

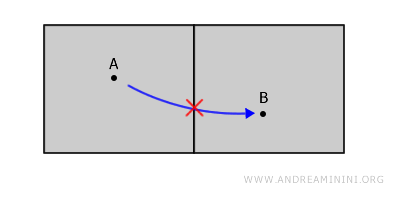
Ovaj jednostavan primjer pokazuje da granice nisu dio otvorenih skupova - zid, dakle, "prekida" povezanost prostora.

Lokalna povezanost

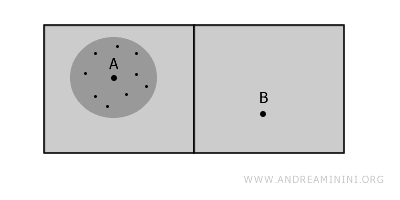
Kažemo da prostor ima lokalnu povezanost ako svaka tačka ima svoje "malo okruženje" koje je povezano, čak i ako cijeli prostor nije.

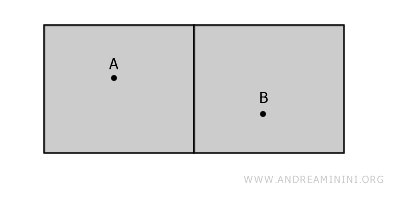
Zamislite opet dvije odvojene sobe. Cijela zgrada kao prostor nije povezana, ali svaka soba zasebno jeste - unutar nje se bilo koje dvije tačke mogu povezati bez prepreka.

Tačka A, na primjer, nalazi se u povezanom podskupu - sobi - i to je primjer lokalne povezanosti.

Isto vrijedi i za tačku B: i ona ima lokalno povezano susjedstvo.

Vrste povezanosti

Povezanost može imati različite oblike. Dvije osnovne vrste su:

• Topološka povezanost
  Topološki prostor $ X $ naziva se povezanim ako ga nije moguće razdvojiti na dva otvorena, disjunktna i neprazna podskupa čiji je zbir cijeli prostor. Drugim riječima, ne postoji način da se prostor “razbije” na dvije odvojene i nezavisne cjeline.

  Primjer. Prostor (-1, 1) je povezan, dok prostor (-1, 0) ∪ (0, 1) nije, jer postoje dva otvorena, disjunktna i neprazna skupa, (-1, 0) i (0, 1), čija unija čini cijeli prostor.
  Ta dva skupa, dakle, predstavljaju razdvajanje prostora.

• Povezanost putem (ili lukom)
  Topološki prostor naziva se povezanim putem ako za svaka dva tačke A i B u prostoru postoji neprekidna putanja koja ih spaja i u potpunosti ostaje unutar tog prostora. Svaki prostor povezan putem nužno je i povezan, iako obrnuto ne mora vrijediti.

  Na primjer, zamisli zatvorenu figuru u ravni. Za bilo koje dvije unutrašnje tačke A i B može se povući neprekidna kriva koja ih povezuje, bez podizanja olovke s papira i bez napuštanja same figure.
  
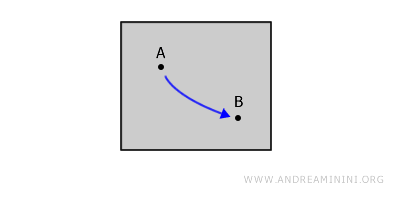
  Razlika između povezanosti lukom i putem.  Povezanost lukom vrlo je slična povezanosti putem, ali u tom slučaju put mora biti injektivan, što znači da se ne smije presijecati niti prolaziti dvaput kroz istu tačku.

• Jednostavna povezanost
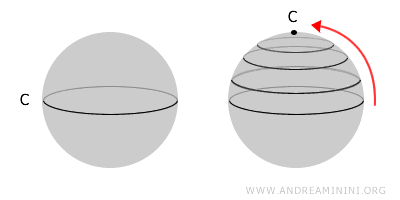
  Prostor je jednostavno povezan ako se svaka zatvorena petlja unutar njega može "stisnuti" do jedne tačke, bez prekidanja kontinuiteta. To znači da prostor nema unutrašnje šupljine. Svaki jednostavno povezan prostor je povezan, ali ne vrijedi obrnuto.

  Sfera je jednostavno povezana: svaka petlja na njenoj površini može se polako skupiti do jedne tačke. Nasuprot tome, torus (krofna) ima otvor u sredini, pa se petlje koje prolaze oko tog otvora ne mogu svesti na tačku - on je povezan, ali ne i jednostavno povezan.
  
  
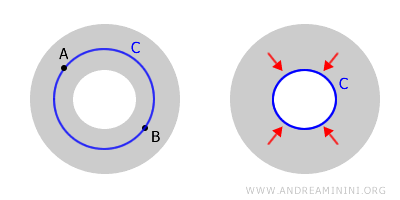
  Takvi prostori, koji su povezani ali ne i jednostavno povezani, nazivaju se višestruko povezani. Klasičan primjer za to je prstenasti prostor.

Napomena

Za kraj, zanimljiv primjer: u skupu realnih brojeva jedini povezani prostori su intervali. Svaki prekid, ma koliko sitan, razbija povezanost.