Povezani prostori u topologiji

Šta znači da je prostor povezan?

Drugim rečima, prostor je povezan ako se ne može „rascepiti“ na dva odvojena dela koji su i otvoreni i neprazni. Kada se to ipak može učiniti, kažemo da je prostor nepovezan, a taj par skupova ( (U, V) ) zovemo razdvajanjem prostora.

Napomena. Ovo je osnovna definicija topološke povezanosti pomoću otvorenih skupova. Kasnije ćemo videti da se ovaj pojam razlikuje od putne povezanosti ili povezanosti lukom - i da nisu uvek ista stvar.

Primer iz prakse

Zamislimo prostor $ X $ koji sadrži tri tačke:

$$ X = {a, b, c} $$

Na ovom skupu možemo definisati dve različite topologije:

• Topologija A
  Otvoreni skupovi su: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topologija B
  Otvoreni skupovi su: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Pitanje: koji od ova dva prostora je povezan?

Po definiciji, topološki prostor ( X ) je povezan ako ne postoje dva neprazna, disjunktna otvorena skupa čiji zbir pokriva ceo prostor. Ako takav par postoji, on čini razdvajanje prostora, i prostor je nepovezan.

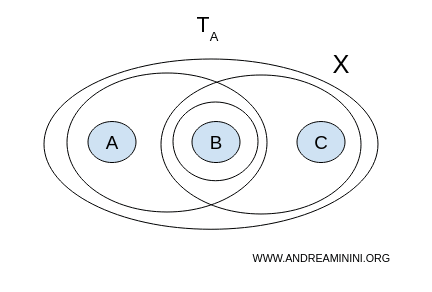
1] Topologija A

Tražimo razdvajanje $ (U, V) $ u topologiji $ \mathcal{T}_A $. Pogledajmo moguće kombinacije:

• $ U = {a,b}, V = {b,c} $ - nisu disjunktni jer sadrže $ b $;
• $ U = {a,b}, V = {b} $ - takođe nisu disjunktni;
• $ U = {b}, V = {b,c} $ - opet nisu disjunktni.

Ne postoji nijedan par nepraznih disjunktnih otvorenih skupova koji pokriva ceo $ X $. Dakle, sa topologijom $ A $, prostor $ X $ je povezan.

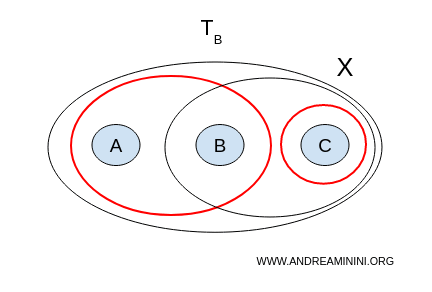
2] Topologija B

Sada proverimo topologiju $ \mathcal{T}_B $:

• $ U = {a,b}, V = {b,c} $ - nisu disjunktni jer sadrže $ b $;
• $ U = {a,b}, V = {c} $ - neprazni su, disjunktni i zajedno pokrivaju $ X $.

Ovaj par ispunjava sve uslove razdvajanja, pa je prostor $ X $ sa topologijom B nepovezan.

Napomena. Ovaj primer jasno pokazuje da povezanost ne zavisi samo od skupa tačaka, već i od same topologije. Isti skup može biti povezan u jednoj topologiji, a nepovezan u drugoj.

Još jedan primer: realna prava bez jedne tačke

Razmotrimo prostor $ X $ gde je $ n $ bilo koji realan broj (npr. $ n = 0 $):

$$ X = (-\infty, n) \cup (n, +\infty) $$

Drugim rečima, to je realna prava iz koje smo izbacili tačku $ n $:

$$ X = \mathbb{R} \setminus {n} $$

Da li je ovaj prostor povezan?

Uzmimo dva skupa: $ U = (-\infty, n) $ i $ V = (n, +\infty) $.

• Oba su otvorena u standardnoj topologiji;
• Disjunktni su, jer ne dele nijednu tačku;
• Neprazni su.

Njihov zbir pokriva ceo prostor $ X $, što znači da prostor možemo razdvojiti na dva otvorena dela. Dakle, $ X $ je nepovezan.

Napomena. Kada uklonimo jednu tačku sa realne prave, ona se „preseca“ na dva nezavisna dela - levo i desno od te tačke. Ti delovi se više ne mogu spojiti kontinuiranom putanjom, pa prostor nije samo nepovezan, već i nije putno povezan.

Povezanost i putna povezanost

Topološka povezanost i putna povezanost često se mešaju, ali nisu isto.

Prostor može biti povezan, a da ipak nije putno povezan (niti povezan lukom).

• Topološka povezanost
  Prostor se ne može podeliti na dva disjunktna, neprazna otvorena podskupa.
• Putna povezanost
  Za svaka dva mesta u prostoru postoji kontinualna putanja koja ih spaja i u potpunosti se nalazi unutar prostora. Ako putanja ne prolazi više puta kroz istu tačku, prostor je povezan lukom.

Važno je zapamtiti: svaki putno povezan prostor je povezan, ali nije svaki povezan prostor putno povezan.

Kontinualna putanja između tačaka sprečava da se prostor „preseče“ na dva otvorena dela. Ali obrnuto ne važi: postoje prostori koji su povezani, ali ne i putno povezani.

Primer. Poznati primer je topologova sinusna kriva: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ Ovaj prostor je povezan jer ga nije moguće razdvojiti na dva disjunktna otvorena skupa, ali nije putno povezan jer ne postoji kontinualna putanja koja bi spojila tačku na oscilujućoj krivoj sa tačkom na vertikalnom segmentu.

I to je samo početak fascinantnog sveta topologije.

Bilješke

Dodatna objašnjenja o povezanim prostorima

• Teorem: karakterizacija povezanih prostora pomoću otvorenih i zatvorenih (clopen) skupova
  Topološki prostor \( X \) je povezan ako i samo ako su jedini njegovi podskupovi koji su istovremeno otvoreni i zatvoreni (clopen) sam prostor \( X \) i prazan skup \( \emptyset \).

Ostala povezana zapažanja mogu se razraditi na sličan način.