Povezanost preko zajedničkog presjeka
Neka su \( C_1, C_2, \dots, C_n \subset X \) povezani podskupovi topološkog prostora \( X \) takvi da je njihov presjek neprazan: \[ \bigcap_{i=1}^n C_i \neq \varnothing . \] Tada je i njihova unija \( \bigcup_{i=1}^n C_i \) povezan skup.
Drugim riječima, ako više povezanih skupova dijeli barem jednu zajedničku točku, njihova unija ostaje povezana. Ta zajednička točka „drži na okupu" cijelu strukturu.
Ova tvrdnja oslanja se na jednostavnu, ali ključnu ideju: postojanje zajedničke točke onemogućuje razdvajanje skupa na dva nepovezana dijela.
Napomena. Uvjet \( \bigcap_{i=1}^n C_i \neq \varnothing \) dovoljan je za povezanost unije \( \bigcup_{i=1}^n C_i \), ali nije nužan. Unija povezanih skupova može ostati povezana i bez jedne zajedničke točke za sve skupove. To se, primjerice, događa kada se skupovi preklapaju postupno ili lančano.
Konkretan primjer
Razmotrimo sljedeće podskupove prostora \( \mathbb{R}^2 \):
- \( C_1 \): horizontalni segment koji povezuje točke \( (-1,0) \) i \( (1,0) \)
- \( C_2 \): vertikalni segment koji povezuje točke \( (0,-1) \) i \( (0,1) \)
- \( C_3 \): dijagonalni segment koji povezuje točke \( (-1,-1) \) i \( (1,1) \)
Svaki od tih skupova pojedinačno je povezan.
Osim toga, svi se sijeku u istoj točki, i to u točki \( (0,0) \):
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
Stoga je njihov zajednički presjek neprazan:
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
Prema prethodnom kriteriju, njihova unija je povezan skup:
\[ C_1 \cup C_2 \cup C_3 \]
Tri se segmenta susreću u jednoj središnjoj točki, što osigurava povezanost cijele figure.
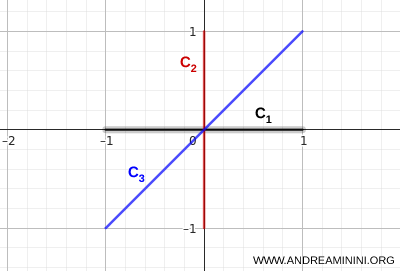
Iz bilo koje točke na jednom segmentu moguće je stići do bilo koje druge točke, a da se pritom ne napusti njihova unija.
Napomena. Postoje i drugi kriteriji povezanosti koji ne zahtijevaju postojanje jedne zajedničke točke za sve skupove. Na primjer, ako su skupovi \( C_i \) povezani i međusobno se preklapaju lančano, odnosno ako vrijedi \( C_i \cap C_{i+1} \neq \varnothing \), tada je njihova unija \( \bigcup_i C_i \) povezana čak i kada vrijedi \( \bigcap_i C_i = \varnothing \). Taj uvjet ipak nije nužan. Unija može ostati povezana i kada su neki uzastopni parovi disjunktni, pod uvjetom da drugi skupovi osiguravaju vezu između njih. Klasičan primjer su tri segmenta koja tvore trokut. Iako je njihov zajednički presjek prazan, \( \bigcap_i C_i = \varnothing \), njihova unija ipak ostaje povezana.
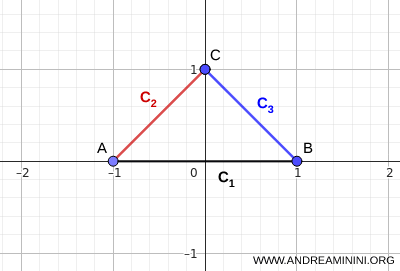
Ovaj primjer jasno pokazuje kako povezanost može nastati kroz lanac lokalnih presjeka.
Dokaz
Neka je \( X \) topološki prostor i neka je \( \{C_i\}_{i \in I} \) familija povezanih podskupova prostora \( X \) čiji je presjek neprazan:
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Pretpostavimo, radi proturječja, da unija
\[ C = \bigcup_{i \in I} C_i \]
nije povezana.
Tada postoje dva otvorena skupa \( U \) i \( V \) koji čine razdvajanje skupa \( C \), odnosno:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Budući da je presjek skupova \( C_i \) neprazan, postoji točka
\[ x \in \bigcap_{i \in I} C_i \]
Ta točka pripada svim skupovima \( C_i \), a time i skupu \( C \). Ona mora pripadati ili skupu \( U \) ili skupu \( V \), ali ne oboma, jer oni čine razdvajanje skupa \( C \). Bez gubitka općenitosti pretpostavimo da vrijedi
\[ x \in U \quad \text{i} \quad x \notin V \]
Budući da je svaki skup \( C_i \) sadržan u \( C \), vrijedi:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
Skupovi \( C_i \cap U \) i \( C_i \cap V \) otvoreni su u induciranoj topologiji na \( C_i \), međusobno su disjunktni i zajedno čine cijeli \( C_i \). Budući da je svaki \( C_i \) povezan, jedan od ta dva skupa mora biti prazan.
Iz toga slijedi da je svaki \( C_i \) u cijelosti sadržan ili u \( U \) ili u \( V \).
Budući da je \( x \in C_i \) i \( x \in U \), nemoguće je da vrijedi \( C_i \subset V \). Stoga vrijedi:
\[ C_i \subset U \quad \text{za svaki } i \in I \]
Prema tome, i sama unija \( C \) sadržana je u skupu \( U \):
\[ \bigcup_{i \in I} C_i \subset U \]
To je u proturječju s pretpostavkom da vrijedi \( V \cap C \neq \varnothing \).
Ova proturječnost pokazuje da je početna pretpostavka pogrešna. Zaključujemo da je unija \( \bigcup_{i \in I} C_i \) povezan skup.