Topologija

Topologija je grana matematike koja proučava svojstva prostora koja ostaju ista čak i kada se taj prostor rasteže, savija ili deformira - sve dok se ne kida i ne lijepi. Takva svojstva uključuju povezanost, kompaktnost i broj „rupa" u objektu.

Drugim riječima, topologija istražuje kako su dijelovi prostora povezani i raspoređeni, ne mareći za mjeru, veličinu ili udaljenost. Bitno je samo ono što se ne mijenja pri neprekidnim deformacijama.

U topologiji pojmovi poput udaljenosti i ugla prestaju biti važni. Umjesto njih, naglasak je na kvaliteti oblika - na tome što ih čini povezanima, neprekinutima i elastičnima.

Središnji pojam topologije jest topološki prostor, a osnovne transformacije koje očuvaju ta svojstva zovu se homeomorfizmi.

Topologiju često nazivaju „gumena geometrija". U njoj se objekti zamišljaju kao izrađeni od elastične tvari koja se može istegnuti ili sabiti, ali ne i pokidati ili zalijepiti. To je jedno od temeljnih područja suvremene matematike.

Povijest

Početci topologije sežu u 18. stoljeće i poznati problem Sedam mostova Königsberga. Leonhard Euler prvi je shvatio da taj zadatak ne ovisi o duljinama mostova ni o točnim udaljenostima, već samo o povezanosti - o tome kako su dijelovi prostora međusobno spojeni.

Problem sedam mostova: U gradu na rijeci postojalo je sedam mostova koji su spajali obale i otoke. Postavlja se pitanje - može li se svaki most prijeći točno jednom, a da se nijedan ne ponovi?

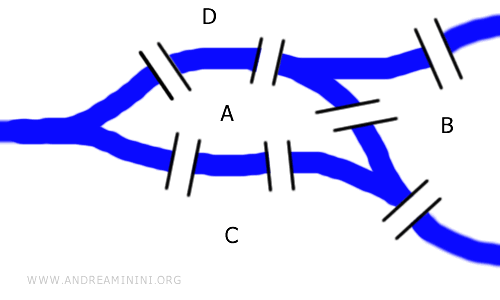
Rješenje ne ovisi o udaljenostima ni o obliku mostova. To je čisti topološki problem koji se može prikazati pomoću grafova. Graf prikazan ovdje topološki je ekvivalentan izvornom rasporedu mostova.

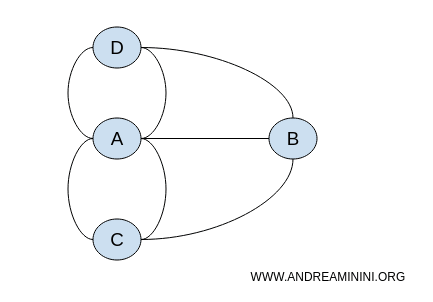
Položaj točaka u grafu nije važan - bitne su samo veze među njima. Zato se isti problem može prikazati bezbrojnim različitim, ali topološki istovjetnim grafovima.

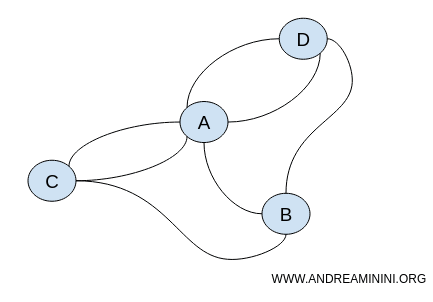
Svi oni imaju ista topološka svojstva: kontinuitet i povezanost.

Eulerov rad otvorio je novo poglavlje u razumijevanju prostora. Pokazao je da geometrijski problemi mogu imati rješenja koja ne ovise o mjerama, već o odnosima među dijelovima prostora - i time je započela „geometrija položaja".

Kasniji matematičari poput Gaussa, Möbiusa, Riemanna i Brouwera proširili su te ideje i oblikovali topologiju kakvu danas poznajemo. Johann Listing prvi je upotrijebio naziv „topologija" 1847. godine.

Tijekom 19. i 20. stoljeća topologija se razvila u više grana - algebarsku, diferencijalnu, opću i geometrijsku - a matematičari poput Poincaréa i Hausdorffa dali su joj čvrste teorijske temelje.

Danas je topologija jedno od ključnih područja matematike koje povezuje apstraktne ideje s vrlo konkretnim primjenama u znanosti, tehnologiji i analizi podataka.

Topološki prostori

Topološki prostor je skup X zajedno sa strukturom T, koja se naziva „topologija". Ona omogućuje matematički opis pojmova kao što su kontinuitet, blizina i granica - bez potrebe za konkretnim mjerenjem.

$$ (X,T) $$

Primjer: Najpoznatiji primjer topološkog prostora je pravac realnih brojeva \( \mathbb{R} \). U standardnoj topologiji skup je otvoren ako sadrži mali interval oko svake svoje točke. Na taj način pojmovi poput kontinuiteta i granica dobivaju jednostavno i intuitivno značenje.

Homeomorfizmi

Homeomorfizam je neprekidna i obostrano jednoznačna transformacija između dvaju topoloških prostora čija je inverzna funkcija također neprekidna. Drugim riječima, prostor se može rastegnuti, saviti ili izobličiti, ali bez rezanja i lijepljenja.

Dva prostora koja se mogu povezati homeomorfizmom smatraju se topološki istovjetnima.

Primjer: Pretvaranje šolje kafe u krofnu klasičan je i zabavan primjer homeomorfizma. Oba objekta imaju jednu rupu i mogu se neprekidnim deformacijama transformisati jedan u drugi, bez narušavanja njihove osnovne strukture.

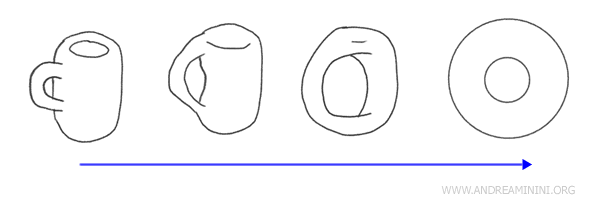
Geometrija i topologija

Iako se bave sličnim pojmovima, geometrija i topologija gledaju svijet iz različitih perspektiva.

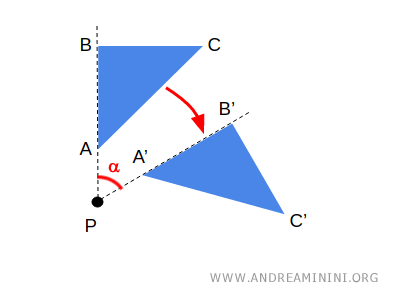
• Geometrija proučava veličine, udaljenosti i kutove. Usredotočuje se na precizne oblike i odnose među njima. Primjerice, rotacija trokuta tipična je geometrijska transformacija jer zadržava duljine stranica.
  

  Euklidska geometrija najpoznatiji je oblik geometrije, dok neeuklidske varijante ispituju svjetove u kojima se mijenja ili negira peti Euklidov postulat o paralelama.

• Topologija proučava ono što ostaje isto i kad se oblici rastegnu, sabiju ili deformiraju. Zanimaju je povezanost i kontinuitet, a ne dimenzije. Na primjer, pretvaranje kocke od gline u kuglu ne mijenja činjenicu da su sve točke povezane u jedinstvenu cjelinu.
  

  Primjer: Ako se glinena kocka sabije u kuglu bez kidanja materijala, rezultat je homeomorfizam - tipična topološka transformacija.
  

Iako polaze od različitih pitanja, geometrija i topologija čvrsto su povezane. Topologija se može smatrati općom, apstraktnijom verzijom geometrije koja se ne bavi mjerenjem, već samom strukturom prostora.

Glavne grane topologije

Topologija danas ima brojne podgrane koje proučavaju različite aspekte prostora i nalaze primjenu u mnogim područjima znanosti.

• Geometrijska topologija: proučava oblike koji se mogu deformirati bez trganja i lijepljenja. Bavi se pojmovima poput kontinuiteta, povezanosti i kompaktnosti.
• Opća topologija (ili topologija skupova točaka): istražuje najopćenitije zakone topoloških prostora i pojmove poput otvorenih i zatvorenih skupova, kontinuiteta i granica.
• Algebarska topologija: povezuje algebru i topologiju - koristi algebarske strukture da bi opisala i razumjela oblik prostora.
• Diferencijalna topologija: proučava prostore koji se lokalno ponašaju kao euklidski prostori i omogućuje definiranje pojmova poput tangente i glatkoće.
• Primijenjena topologija: koristi topološke metode u praktičnim područjima - od analize podataka i mreža do biologije i inženjerstva.

Svaka od ovih grana ima vlastite metode i ciljeve, ali sve dijele istu ideju: razumjeti strukturu prostora iza oblika koje vidimo.