Otvoreni skupovi u topologiji
Skup A naziva se otvorenim ako za svaki element x koji pripada skupu (x∈A) postoji okolina te tačke koja je u potpunosti sadržana u skupu.
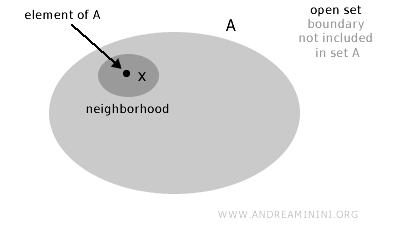
Drugim riječima, skup je otvoren ako njegove granične tačke, intuitivno posmatrano, ne pripadaju samom skupu.
Formalno, skup A u topološkom prostoru X otvoren je ako za svaku tačku x iz A postoji okolina te tačke koja je u potpunosti unutar A.
Napomena. To znači da se oko svake tačke skupa može pronaći okolina koja u potpunosti ostaje unutar skupa, bez dodirivanja njegove spoljne granice.
Praktičan primjer
Jedan od najjednostavnijih primjera otvorenog skupa na realnoj pravoj jeste otvoreni interval.
Šta je otvoreni interval? Otvoreni interval u R je skup realnih brojeva x takvih da važi a < x < b, gdje su a i b realni brojevi i pri tome važi a < b.
Ovaj interval označava se s (a,b). Okrugle zagrade pokazuju da krajnje tačke a i b nisu elementi skupa.
Na primjer, interval (3,10) otvoren je skup na realnoj pravoj.
U ovom slučaju skup A sadrži beskonačno mnogo brojeva između 3 i 10, isključujući sami početak i kraj intervala.
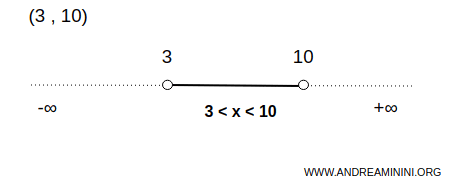
To znači da za svaku tačku x unutar intervala uvijek postoji neki manji otvoreni interval oko te tačke koji u potpunosti ostaje unutar (3,10).
Na primjer, za tačku x = 3.1 možemo uzeti otvoreni interval (3.09,3.11), koji je u potpunosti sadržan u (3,10).
Ista logika vrijedi za svaku drugu tačku unutar intervala (3,10), jer između bilo koja dva realna broja postoji beskonačno mnogo drugih realnih brojeva.
Napomena. Čak i ako posmatram veoma mali broj unutar intervala, na primjer 3.001, mogu konstruisati okolinu 3.001±0.00000001 koja i dalje sadrži beskonačno mnogo realnih brojeva smještenih unutar otvorenog intervala (3,10).
Ovo je osnovni jednodimenzionalni primjer otvorenog skupa.
Drugi primjeri
Isti koncept važi i u dvodimenzionalnom prostoru, na primjer u ravni.
Posmatrajmo skup svih tačaka unutar kruga poluprečnika r = 1 sa centrom u koordinatnom početku (0,0).
$$ x^2+y^2<1 $$
Ova nejednakost opisuje sve tačke čija je udaljenost od centra manja od 1. Dakle, obod kruga nije uključen, već samo unutrašnjost.
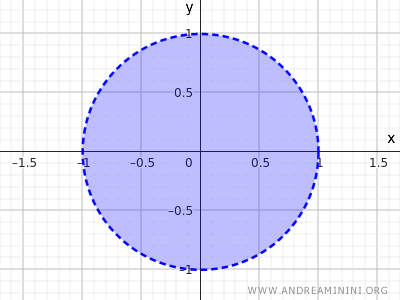
To je još jedan tipičan primjer otvorenog skupa.
Kada je skup zatvoren?
Da bismo dobili zatvoren skup, dovoljno je uključiti i tačke na obodu kruga.
$$ x^2+y^2 \le 1 $$
U tom slučaju uslov o postojanju okoline koja u potpunosti ostaje unutar skupa više nije ispunjen za svaku tačku.
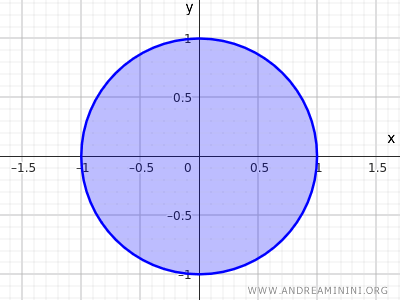
Tačke na obodu kruga tada nemaju okolinu koja ostaje u potpunosti unutar skupa, pa on nije otvoren.
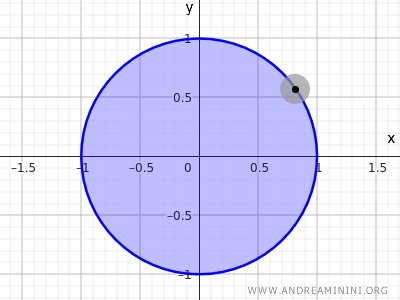
Napomena. U topologiji skup definisan jednačinom \( x^2+y^2=1 \) nije otvoren niti zatvoren u euklidskom prostoru R2, jer sadrži samo tačke na obodu i nijednu tačku iz unutrašnjosti. Međutim, skup definisan nejednakošću \( x^2+y^2<1 \) otvoren je skup, dok uključivanjem i oboda, \( x^2+y^2\le 1 \), dobijamo zatvoren skup.
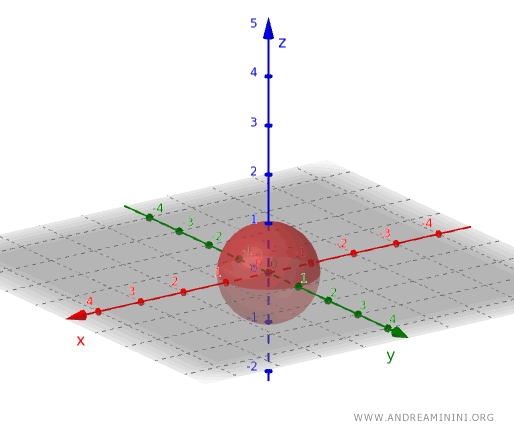
Isti princip vrijedi i u trodimenzionalnom prostoru. Na primjer, otvoreni skup dobijamo ako posmatramo sve tačke unutar sfere, isključujući one koje leže na njenoj površini.
Odabir topologije
Otvoreni intervali korisni su jer daju intuitivnu predstavu o tome šta je otvoreni skup.
Ipak, pojam otvorenog skupa je apstraktniji i nije ograničen samo na intervale ili geometrijske primjere.
Kada se osnovna ideja shvati, potrebno je produbiti razumijevanje.
Pojam otvorenog skupa uvijek zavisi od topologije koju primjenjujemo na prostor.
Ključno je razumjeti da definicija otvorenih skupova može u potpunosti zavisiti od izbora topologije.
U nekim prostorima skup koji izgleda zatvoren u standardnoj topologiji može biti otvoren u nekoj drugoj.
Drugim riječima, isti skup može biti otvoren ili neotvoren, zavisno od topologije koju usvojimo.
Šta je topologija? Topologija na prostoru je kolekcija podskupova koji se smatraju otvorenim i koji zadovoljavaju određena pravila. Na primjer, proizvoljna unija otvorenih skupova mora biti otvoren skup, a presjek konačno mnogo otvorenih skupova takođe mora biti otvoren.
Zato ne treba zaključivati o otvorenim skupovima samo na osnovu najpoznatijih primjera kao što su otvoreni intervali ili otvoreni diskovi.
U topologiji pojam otvorenog skupa je mnogo širi i obuhvata i skupove koji se na prvi pogled možda ne bi smatrali otvorenima.
Praktičan primjer
Posmatrajmo prostor \( \{a, b\} \) koji sadrži samo dva elementa.
Nad ovim prostorom možemo definisati najmanje dvije različite topologije: trivijalnu i diskretnu.
- Trivijalna topologija
U trivijalnoj topologiji jedini otvoreni skupovi su prazni skup \( \emptyset \) i cijeli prostor \( \{a, b\} \). Ovo je najosnovnija topologija, jer praktično ne sadrži nikakvu dodatnu strukturu. - Diskretna topologija
U diskretnoj topologiji svaki podskup od \( \{a, b\} \) smatra se otvorenim. To znači da su \( \{a\} \), \( \{b\} \), \( \{a, b\} \) i \( \emptyset \) svi otvoreni skupovi. Diskretna topologija je najbogatija jer omogućava najviše otvorenih skupova.
Sada posmatrajmo skup \( \{a\} \) u obje topologije:
- U trivijalnoj topologiji skup {a} nije otvoren
Jedini otvoreni skup koji sadrži elemente je \( \{a, b\} \), pored praznog skupa. - U diskretnoj topologiji skup {a} jeste otvoren
U ovoj topologiji svaki podskup, uključujući \( \{a\} \) i \( \{b\} \), otvoren je po definiciji.
Prema tome, skup \( \{a\} \) otvoren je u diskretnoj, ali nije otvoren u trivijalnoj topologiji.
Ovaj jednostavan primjer jasno pokazuje da je pojam otvorenog skupa neraskidivo vezan za izbor topologije.
Teorem o otvorenim skupovima
Teorem 1
Neka je X otvoren skup, a T topologija tako da zajedno čine topološki prostor (X,T). Podskup S⊂X je otvoren u prostoru (X,T) ako za svaku tačku s∈S postoji okolina U koja je u potpunosti sadržana u S, odnosno U⊂S.
Po definiciji, S je otvoren skup jer pripada topološkom prostoru (X,T).
Zbog toga se podskup S može posmatrati kao okolina svake svoje tačke s∈S.
Iz toga slijedi da je okolina Us svake tačke s∈S takođe otvoren skup sadržan unutar S.
$$ x \in U_s \subset S \subset X $$
Otvoren skup možemo posmatrati kao uniju otvorenih okolina svojih tačaka.
Ako svaka tačka s∈S posjeduje okolinu Us⊂S koja ostaje u potpunosti unutar S, zaključujemo da je S otvoren skup jer je unija otvorenih skupova.
Drugim riječima, skup je otvoren ako i samo ako za svaku tačku u njemu postoji okolina koja je u potpunosti sadržana u tom skupu.
Primjer. Zamislite sto na kojem se nalaze staklene kuglice. Svaka kuglica predstavlja tačku skupa. Reći da je skup „otvoren" znači da oko svake kuglice postoji dovoljno prostora da se može kretati, a da ne dodirne ivicu stola. Ako je oko svake kuglice moguće nacrtati krug koji u potpunosti ostaje na površini stola, tada skup kuglica predstavlja „otvoren skup". Suština je jednostavna: koju god kuglicu odaberemo, uvijek postoji dio prostora oko nje koji još pripada tom istom skupu.

Teorem 2
Neka je \( X \) skup i neka \( B \) predstavlja bazu topologije na \( X \). Podskup \( A \subset X \) je otvoren u topologiji generisanoj bazom \( B \) ako i samo ako za svaku tačku \( x \in A \) postoji bazni skup \( B_x \) koji sadrži \( x \) i koji je u potpunosti sadržan u \( A \), odnosno \( B_x \subseteq A \).
Ovaj teorem naglašava ključnu osobinu topologija koje se određuju pomoću baze.
Drugim riječima, svaka tačka otvorenog skupa \( A \) mora imati „okolinu" \( B_x \) iz baze, koja se u potpunosti nalazi unutar \( A \).
Na taj način potvrđujemo da je \( A \) otvoren skup u topologiji definisanoj bazom \( B \).
Dokaz. Ako je A otvoren skup u topologiji generisanoj bazom \( B \), tada je A unija baznih skupova. Dakle, svaka tačka \( x \in A \) pripada barem jednom baznom skupu \( B_x \), i taj \( B_x \) je u potpunosti unutar A. Obrnuto, ako svaka tačka \( x \in A \) pripada nekom baznom skupu \( B_x \) koji je u potpunosti sadržan u A, tada je A unija takvih skupova i samim tim otvoren.
Primjer
Uzmimo skup \( X = \{1, 2, 3, 4, 5\} \) i bazu topologije nad njim \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). Želimo provjeriti da li je skup \( A = \{1, 2, 3\} \) otvoren.
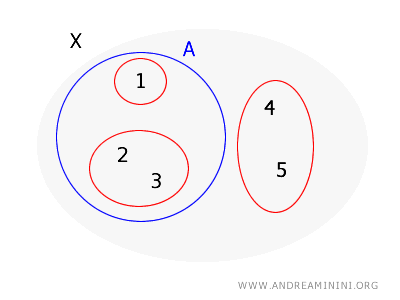
Za svaku tačku iz \( A \) potrebno je pronaći bazni skup koji je sadrži i koji se u potpunosti nalazi unutar \( A \):
- Za tačku \( 1 \) postoji bazni skup \( \{1\} \), koji je u potpunosti unutar \( A \).
- Za tačku \( 2 \) postoji bazni skup \( \{2, 3\} \), koji je u potpunosti sadržan u \( A \).
- Za tačku \( 3 \) vrijedi isto: bazni skup \( \{2, 3\} \) u potpunosti je unutar \( A \).
Budući da svaka tačka iz \( A \) ima pripadajući bazni skup unutar \( A \), uslov teorema je ispunjen.
Zato zaključujemo da je \( A \) otvoren skup u topologiji generisanoj bazom \( B \).
Primjer 2
Razmotrimo isti skup \( X = \{1, 2, 3, 4, 5\} \) i istu bazu \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \).
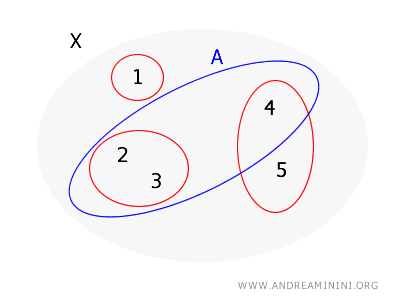
Provjeravamo sada skup \( A = \{2, 3, 4\} \).
- Za tačku \( 2 \) bazni skup \( \{2, 3\} \) nalazi se u potpunosti u \( A \).
- Isto važi i za tačku \( 3 \).
- Za tačku \( 4 \) ne postoji bazni skup koji bi je obuhvatao, a da se u potpunosti nalazi unutar \( A \), jer je jedini bazni skup sa 4 skup \( \{4, 5\} \), koji sadrži element koji nije u \( A \).
Prema tome, skup \( A \) nije otvoren u topologiji generisanoj bazom \( B \), jer ne ispunjava uslov da svaka njegova tačka ima bazni skup potpuno sadržan u \( A \).
I tako dalje.