Zatvoreni skupovi

Kažemo da je skup $ B $ u topološkom prostoru $ X $ zatvoren ako za svaku točku komplementa $ u \in X - B $ postoji okolina koja je u potpunosti sadržana u tom komplementu $ X - B $.
primjer zatvorenog skupa

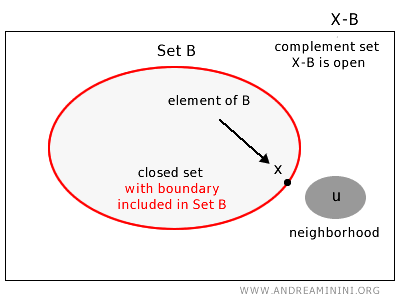
Drugim riječima, skup je zatvoren ako sadrži sve svoje granične točke.

Preciznije, skup $ B $ u topološkom prostoru $ X $ je zatvoren ako je njegov komplement $ X - B $ otvoren skup.

Napomena: To znači da u $ B $ postoji barem jedna točka oko koje nijedna okolina ne može biti u potpunosti sadržana u $ B $.

Konkretniji primjer
Komplement zatvorenog skupa
Primjer
Svojstva zatvorenih skupova
Primjer
Dodatne napomene

Konkretniji primjer

Razmotrimo realnu pravu $ \mathbb{R} $ i zatvoreni interval.

Što je zatvoreni interval? Zatvoreni interval u $ \mathbb{R} $ je skup svih točaka $ x $ za koje vrijedi $ a \leq x \leq b $, gdje su $ a $ i $ b $ realni brojevi s $ a < b $, pri čemu su obje granice uključene.

Takav se interval označava s $[a,b]$. Uglaste zagrade upućuju na to da krajnje točke $ a $ i $ b $ pripadaju skupu.

Na primjer, zatvoreni interval $[3,10]$ predstavlja zatvoreni skup na realnoj pravoj $ \mathbb{R} $.

U ovom slučaju skup $ B $ obuhvaća sve brojeve između 3 i 10, uključujući krajnje vrijednosti.

primjer zatvorenog intervala

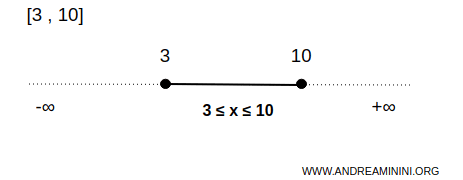
Drugim riječima, svaka točka $ x $ koja zadovoljava $ 3 \leq x \leq 10 $ pripada skupu, uključujući krajnje točke $ x=3 $ i $ x=10 $.

Ipak, nije nužno da sve točke imaju okolinu u potpunosti sadržanu u intervalu $[3,10]$.

Na primjer, svaka okolina donje granice $ x=3 $ nužno će sadržavati i točke manje od 3, koje ne pripadaju intervalu.

Napomena: Čak i ako izaberemo iznimno malu okolinu, poput $ 3 \pm 0{,}00000001 $, ona neće biti u potpunosti sadržana u intervalu $[3,10]$ jer je $ 3 - 0{,}00000001 < 3 $. Isto vrijedi i za gornju granicu $ x=10 $, kojoj također ne možemo pridružiti okolinu potpuno sadržanu u intervalu.

Ovo je jednostavan primjer zatvorenog skupa u jednodimenzionalnom prostoru.

Drugi primjeri zatvorenih skupova

Istu ideju možemo proširiti na ravninu $\mathbb{R}^2$.

Razmotrimo, na primjer, skup svih točaka unutar diska polumjera $ r=1 $ sa središtem u $(0,0)$:

$$ x^2 + y^2 \leq 1 $$

Ova nejednakost opisuje sve točke čija je udaljenost od središta $(0,0)$ manja ili jednaka 1, obuhvaćajući unutrašnjost diska i sve točke na kružnici.

zatvoreni skup u ravnini

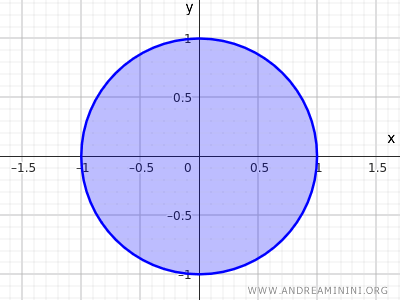
To je još jedan tipičan primjer zatvorenog skupa.

Kao što vidimo, točke na kružnici $ x^2 + y^2 = 1 $ nemaju okolinu u potpunosti sadržanu u zatvorenom disku.

primjer zatvorenog skupa

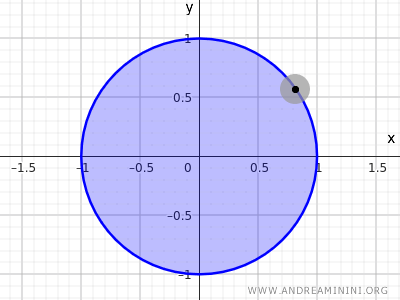
Napomena: U topologiji, kružnica definirana jednadžbom $ x^2 + y^2 = 1 $ nije otvoren ni zatvoren skup u euklidskom prostoru $ \mathbb{R}^2 $ jer sadrži samo točke kružnice, bez unutrašnjosti. Nasuprot tome, skup $ x^2 + y^2 \leq 1 $, koji uključuje i unutrašnjost i kružnicu, jest zatvoren jer sadrži sve svoje granične točke.

Slično tome, pojam zatvorenog skupa proteže se i na trodimenzionalni prostor sa zatvorenom sferom, kao i na $ n $-dimenzionalne prostore sa zatvorenim $ n $-sferama.

Komplement zatvorenog skupa

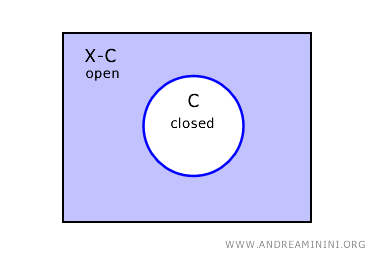
U topološkom prostoru $ X $ komplement zatvorenog skupa $ C $ otvoreni je skup, označen s $ X - C $.

Ako je $ C $ zatvoren u $ X $, njegov komplement $ X - C $ nužno je otvoren.

komplement zatvorenog skupa

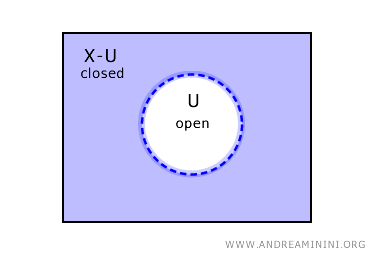
Obrnuto, ako je skup $ U $ otvoren, njegov komplement $ X - U $ zatvoren je skup u $ X $.

komplement otvorenog skupa

Međutim, to nisu jedine mogućnosti. U nekim topološkim prostorima postoje skupovi koji su istovremeno otvoreni i zatvoreni te skupovi koji nisu ni otvoreni ni zatvoreni.

Drugim riječima, činjenica da skup nije zatvoren ne znači automatski da je otvoren, i obrnuto, skup koji nije otvoren ne mora biti zatvoren.

Primjer

Razmotrimo topološki prostor $ (X, T) $, gdje skup $ X = \{a,b,c,d\} $ ima četiri elementa, a topologija $ T $ zadana je sljedećim otvorenim skupovima:

primjer topologije

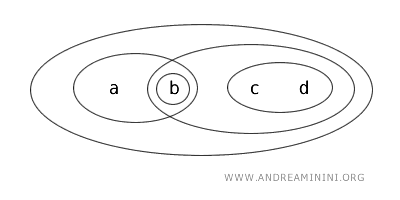
Otvoreni skupovi ove topologije su: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ i prazni skup $ \varnothing $.

Pogledajmo nekoliko karakterističnih slučajeva:

Skup $ \{b\} $ je otvoren jer je izričito naveden kao otvoren u topologiji.
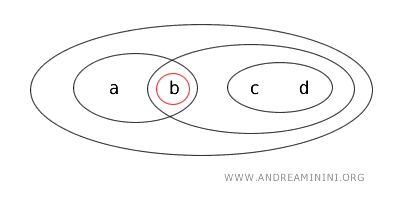
Skup $ \{a\} $ je zatvoren jer je njegov komplement otvoren. Doista, $ X - \{a\} = \{b,c,d\} $ otvoren je skup.
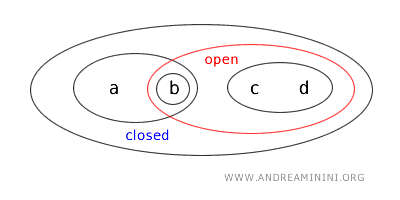
Skup $ \{a,b\} $ je istovremeno otvoren i zatvoren (clopen). Iako je to rijetko u standardnim topologijama na $ \mathbb{R} $, u općenitijim topološkim prostorima moguće je da skup bude i otvoren i zatvoren ako mu je komplement također otvoren. Ovdje je $ \{a,b\} $ otvoren po definiciji topologije, a njegov komplement $ \{c,d\} $ također je otvoren, pa je skup i zatvoren.
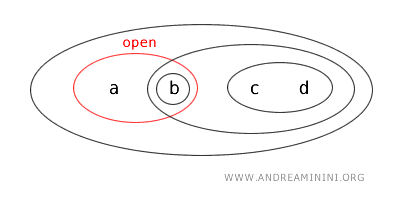
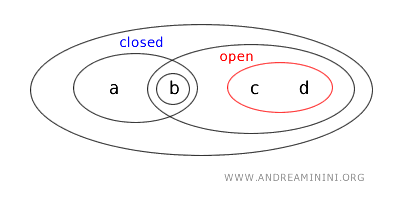
Skup $ \{b,c\} $ nije ni otvoren ni zatvoren. Ne pojavljuje se među otvorenim skupovima, a njegov komplement $ \{a,d\} $ također nije otvoren, pa skup ne ispunjava uvjete ni za otvorenost ni za zatvorenost.

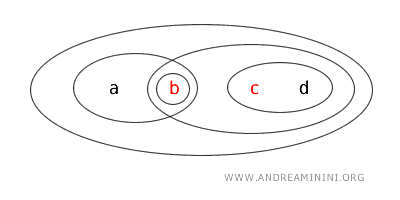
Ovaj primjer jasno pokazuje da skup u topološkom prostoru može biti otvoren, zatvoren, i jedno i drugo (clopen), ili nijedno od navedenog.

Svojstva zatvorenih skupova

Zatvoren skup definira se kao komplement otvorenog skupa. Najvažnija svojstva zatvorenih skupova su:

Prazni skup ($\varnothing$) i cijeli prostor $ X $ uvijek su zatvoreni skupovi.
Presjek bilo koje kolekcije (konačne ili beskonačne) zatvorenih skupova također je zatvoren.
Unija konačno mnogo zatvorenih skupova ostaje zatvorena.

Primjer

U standardnoj topologiji euklidskog prostora $ \mathbb{R}^n $, svaka izolirana točka čini zatvoren skup.

Uzmemo li točku $ n $ na realnoj pravoj ($ \mathbb{R}^1 $), njezin komplement čini skup svih točaka iz $ \mathbb{R}^1 $ osim same točke $ n $.

primjer zatvorenog skupa

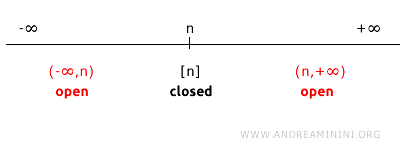
Komplement skupa $\{n\}$ jednak je uniji dvaju otvorenih intervala: $(-\infty, n) \cup (n, +\infty)$.

Budući da su intervali $(-\infty, n)$ i $(n, +\infty)$ otvoreni u standardnoj topologiji, njihova unija $(-\infty, n) \cup (n, +\infty)$ također je otvoren skup.

Prema tome, $\{n\}$ je zatvoren skup jer mu je komplement otvoren.

Ipak, u ostalim topologijama izolirane točke ne moraju uvijek biti zatvoreni skupovi. To u potpunosti ovisi o topološkoj strukturi promatranog prostora.

Razmotrimo topologiju na $ \mathbb{R} $, generiranu skupovima oblika $ (n, n+1) $ za svaki cijeli broj $ n $. U takvoj topologiji izolirane točke $ n $ nisu zatvoreni skupovi jer se ne mogu prikazati kao komplement nekog otvorenog skupa.
primjer topologije
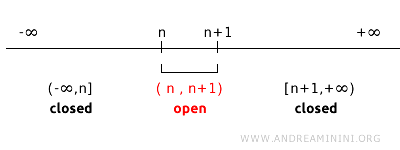
Primjerice, skupovi $ (1,2) $ i $ (2,3) $ otvoreni su u toj topologiji. Njihovi komplementi imaju oblik $ (-\infty, 1] \cup [2, +\infty) $, odnosno $ (-\infty, 2] \cup [3, +\infty) $.

U ovoj topologiji ne postoji otvoren skup čiji je komplement upravo $\{2\}$. Općenito, za svaki otvoreni skup $ (n, n+1) $, njegov komplement je uvijek unija zatvorenih intervala $ (-\infty, n] \cup [n+1, +\infty) $. Zbog toga izolirane točke $ n $ u ovoj topologiji nisu zatvoreni skupovi. Ovaj primjer jasno pokazuje koliko pojam zatvorenog skupa ovisi o odabranoj topologiji.

Dodatne napomene

Slijedi nekoliko korisnih pojmova povezanih sa zatvorenim skupovima:

Zatvoreni skupovi i skupovi nakupljanja
Točka nakupljanja skupa je točka čija svaka okolina, bez obzira koliko mala bila, sadrži barem jednu drugu točku promatranog skupa. Ta je osobina usko povezana sa zatvorenim skupovima jer je skup zatvoren upravo onda kada sadrži sve svoje točke nakupljanja.

Primjer: razmotrimo zatvoreni interval $[0,1]$ na realnoj pravoj. Ovaj skup sadrži sve svoje točke nakupljanja.

Na primjer, točka $0{,}5$ unutar intervala $[0,1]$ ima svaku svoju okolinu koja obuhvaća beskonačno mnogo drugih točaka tog intervala, što potvrđuje da je riječ o točki nakupljanja.
primjer točke nakupljanja u intervalu [0,1]

Isto vrijedi i za krajnje točke. Na primjer, točka $0$ jest točka nakupljanja intervala $[0,1]$ jer svaka njezina okolina sadrži druge točke intervala poput $0{,}1$, $0{,}01$, $0{,}001$ i tako dalje.
krajnje točke intervala [0,1] kao točke nakupljanja
Dakle, sve točke intervala $[0,1]$ točke su nakupljanja tog skupa.

Skup $ A $ je zatvoren ako i samo ako $ A = \overline{A} $
U topološkom prostoru skup $ A $ je zatvoren ako je jednak svojoj zatvorenoj ovojnici, odnosno $ A = \overline{A} $. Zatvorena ovojnica $ \overline{A} $ sastoji se od svih točaka skupa $ A $ zajedno s njegovim točkama nakupljanja. Ako skup $ A $ sadrži sve svoje točke nakupljanja, tada je zatvoren.

I tako dalje.