Otvorena kugla

U topologiji se otvorena kugla, poznata i kao kružno susjedstvo, disk ili otvorena sfera, definira kao skup svih tačaka čija je udaljenost od određene tačke, centra $ c $, strogo manja od polumjera $ r $: $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Ovaj pojam pripada teoriji metričkih prostora $ M $. U takvom prostoru metrika $ d $ određuje kolika je udaljenost između dviju tačaka. Drugim riječima, metrika daje način da se mjeri „blizina" unutar prostora.

Otvorena kugla potpuno je određena samo dvama elementima: njenim centrom i polumjerom.

Kugla je „otvorena" zato što svaka tačka u njoj ima svoju vlastitu, manju otvorenu kuglu koja i dalje ostaje unutar početne kugle. To je temeljna ideja topološke otvorenosti.

Napomena: Otvorene kugle ostaju iste s topološkog stanovišta, čak i kada ih transliramo ili skaliramo. Njihova topološka priroda ne ovisi o mjestu ni veličini.

Posmatrajmo sada ravan $ \mathbb{R}^2 $. Udaljenost između tačke $ p = (x, y) $ i centra $ c = (x_0, y_0) $ određuje se standardnom euklidskom formulom:

$$ d(p,c) = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$

Otvorene kugle imaju ključnu ulogu u opisivanju topološke strukture metričkih prostora. Upravo one čine osnovu standardne topologije ravni $ \mathbb{R}^2 $, što znači da se cijela topologija može izgraditi polazeći od njih.

Ta se struktura opisuje sljedećom familijom skupova:

$$ B = \{ B(p, r) \mid p \in \mathbb{R}^2,\ r > 0 \} $$

Ovdje $ p $ predstavlja bilo koju tačku u ravni, a $ r $ je polumjer otvorene kugle.

standardna topologija u R^2

Među svim mogućim topologijama na $ \mathbb{R}^2 $, euklidska topologija, ona koju određuju otvorene kugle, najčešća je i služi kao standard u matematici.

Unutar otvorene kugle $ B(p,r) $, svaka tačka $ q $ može biti centar nove, manje kugle $ B(q,\epsilon) $ koja se u potpunosti nalazi u većoj kugli. Ovaj lokalni princip ključan je za razumijevanje topološke strukture.

Formalno, to izgleda ovako:

$$ \forall\ q \in B(p,r),\ \exists\ \epsilon > 0\ \text{takvo da}\ B(q,\epsilon) \subset B(p,r) $$

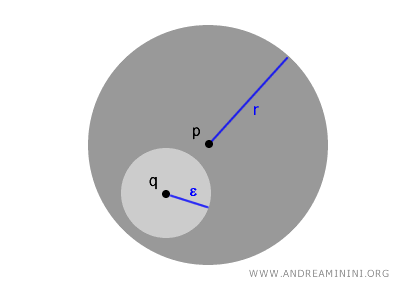
primjer otvorene kugle

Ovaj proces možemo ponavljati neograničeno. Time se jasno vidi koliko je pojam otvorene kugle važan za razumijevanje lokalnih svojstava topoloških prostora i načina na koji se oni „grade" iz svojih najmanjih susjedstava.