Normalni prostor
U topologiji kažemo da je prostor \( X \) normalan kada ispunjava dva osnovna uvjeta:
- Svaki singlton je zatvoren skup
Za svaku točku \( x \in X \), skup \(\{x\}\) mora biti zatvoren. Ovo je važna polazna tačka za razumijevanje separacije u prostoru. - Disjunktni zatvoreni skupovi mogu se odvojiti disjunktnim otvorenim skupovima
Ako su \( A \) i \( B \) zatvoreni skupovi i pri tome nemaju zajedničkih tačaka, postoje otvoreni skupovi \( U \) i \( V \) koji ih potpuno razdvajaju:
- \( A \subset U \)
- \( B \subset V \)
- \( U \cap V = \emptyset \)
Ovaj uvjet je ključni pokazatelj koliko je topološki prostor dobro strukturiran.
Ideja normalnosti može se sažeti ovako: kada imamo dva zatvorena skupa koji se ne dodiruju, uvijek ih možemo "smjestiti" u dva otvorena skupa koji ostaju potpuno odvojeni. Ovo svojstvo posebno je značajno u analizi i konstrukciji neprekidnih funkcija koje razlikuju tačke ili skupove.
Primjer koji sve pojašnjava
Uzmimo najpoznatiji topološki prostor: realnu pravu \( \mathbb{R} \) s uobičajenom topologijom. Otvoreni intervali \( (a, b) \) služe kao osnovni gradivni elementi.
Razmotrimo dva zatvorena skupa koja se međusobno ne dodiruju:
- \( A = \{0\} \)
- \( B = [2, 3] \)
Oba skupa su zatvorena, a između njih postoji jasan razmak.
Napomena. Singlton \( A \) je zatvoren jer sadrži samo jednu tačku, dok je interval \( B \) zatvoren po definiciji.
Da bismo pokazali da je \( \mathbb{R} \) normalan prostor, dovoljni su konkretni otvoreni skupovi koji razdvajaju \( A \) i \( B \).
Za skup \( A \) logičan izbor je otvoreni interval \( U = (-1, 1) \), koji nesumnjivo sadrži točku \( 0 \).
$$ A \subset U = (-1,1) $$
Za skup \( B = [2,3] \) možemo uzeti otvoreni skup \( V = (1, 4) \), koji ga u potpunosti obuhvata.
$$ B \subset V = (1,4) $$
Kada pogledamo ova dva otvorena intervala, jasno je da se ne dodiruju. To znači da vrijedi \( U \cap V = \emptyset \), što potvrđuje normalnost realne prave.
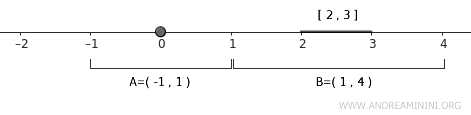
Ovaj jednostavan primjer ilustrira osnovnu ideju: kad god imamo dva disjunktna zatvorena skupa, uvijek možemo pronaći dva otvorena koja ih široko i sigurno razdvajaju.
Zašto je normalnost važna
Normalni prostori igraju ključnu ulogu u općoj topologiji. Neka od najvažnijih svojstava su:
- Realna prava \( \mathbb{R} \) je normalan prostor
Osim što je regularna, ispunjava i snažniji uvjet normalnosti. - Svi metrički prostori su normalni
Ako prostor dolazi s definiranom metrikom, normalnost automatski slijedi. Metrika omogućava vrlo precizno odvajanje skupova. - Normalnost implicira regularnost
Svaki normalan prostor je nužno regularan, iako suprotno ne mora vrijediti.
Ova svojstva čine normalne prostore jednim od temeljnih pojmova u teoriji separacijskih aksiona i ključnim alatom za razumijevanje strukture topoloških prostora.