Homeomorfizmi u topologiji

Homeomorfizam je topološka transformacija predstavljena funkcijom koja je istovremeno bijektivna i neprekidna, a čija je inverzna funkcija takođe neprekidna.

Drugim riječima, jedan se prostor može preoblikovati u drugi, a zatim vratiti u prvobitni oblik bez ikakvog prekida ili dodavanja novih dijelova.

Jednostavno rečeno, homeomorfizam omogućava prelazak iz jednog prostora u drugi na neprekidan način, bez promjene njegove osnovne strukture.

Na primjer, šoljica za kafu s drškom i krofna (torus) su homeomorfni objekti u topološkom smislu. Jedan se može neprekidno deformisati u drugi i obrnuto.

Sa topološkog stanovišta, ove forme su ekvivalentne jer obje imaju po jednu „rupu" - središnju rupu krofne i prostor unutar drške šolje. Mogli bismo zamisliti kako se šolja modeluje oko svoje drške dok ne poprimi oblik krofne.

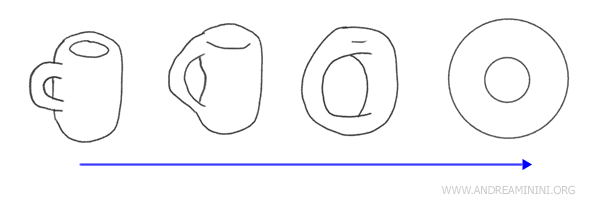
Kada su dva topološka prostora povezana homeomorfizmom, nazivaju se homeomorfni prostori. To znači da su, s topološkog gledišta, suštinski isti, iako se njihove geometrijske forme mogu razlikovati.

Osnovne osobine homeomorfizma

Slijede temeljna svojstva koja definišu homeomorfizam:

• Bijektivnost
  Svakom elementu jednog prostora odgovara tačno jedan element drugog prostora i obrnuto.
• Neprekidnost
  Homeomorfizam je po definiciji neprekidna funkcija: male promjene na ulazu proizvode male promjene na izlazu.
• Neprekidnost inverzne funkcije
  Inverzna funkcija mora biti neprekidna, što obezbjeđuje mogućnost povratne transformacije bez narušavanja kontinuiteta.
• Očuvanje topoloških svojstava
  Homeomorfizam čuva osnovna topološka svojstva kao što su neprekidnost, povezanost i kompaktost. Time se odnosi između tačaka izvornog prostora u potpunosti prenose na transformisani prostor.

Ukratko, homeomorfizam je neprekidna i bijektivna funkcija između dva topološka prostora \(X\) i \(Y\), čija je inverzna funkcija takođe neprekidna. Zahvaljujući tome, topološka svojstva oba prostora ostaju ista.

Drugim riječima, homeomorfizam omogućava „preoblikovanje" jednog prostora u drugi bez kidanja ili lijepljenja dijelova. To je oblik savršene topološke ekvivalencije između dvije prostorne strukture.

Topološka definicija neprekidnosti glasi:

Neka su \(X\) i \(Y\) topološki prostori. Funkcija \(f : X \to Y\) je neprekidna ako za svaki otvoreni skup \(V\) u \(Y\) inverzna slika \(f^{-1}(V)\) pripada otvorenim skupovima u \(X\).

Drugim riječima, neprekidna funkcija u topologiji čuva strukturu otvorenih skupova pri prelasku iz jednog prostora u drugi.

Pojam neprekidnosti u topologiji je apstraktniji i opštiji od onoga u matematičkoj analizi.

Napomena: U analizi, neprekidnost se definiše pomoću rastojanja između tačaka, dok se u topologiji zasniva isključivo na strukturi otvorenih skupova, bez pozivanja na pojam distance.

Ilustrativan primjer

Da bismo intuitivno razumjeli pojmove neprekidnosti i homeomorfizma, razmotrimo ih kroz primjer otvorenih skupova.

Posmatrajmo dva topološka prostora: \(X = \{a, b, c, d\}\) i \(Y = \{1, 2\}\).

• U prostoru \(X\) otvoreni skupovi su: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• U prostoru \(Y\) otvoreni skupovi su: \(\{\}, \{1\}, \{1, 2\}\).

Funkcija \(f : X \to Y\) je neprekidna ako je inverzna slika svakog otvorenog skupa u \(Y\) otvoreni skup u \(X\).

Definišimo funkciju \(f\) na sljedeći način:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Radi lakšeg razumijevanja, predstavićemo funkciju \(f\) i topološke prostore pomoću dijagrama u kojem su otvoreni skupovi prikazani kružnicama.

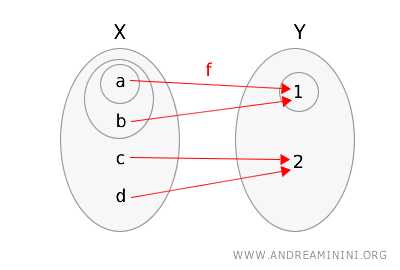
Provjerimo definiciju neprekidnosti:

• Otvoreni skup \(\{1\}\) u \(Y\) ima inverznu sliku \(f^{-1}(\{1\}) = \{a, b\}\), koja je otvorena u \(X\).
• Otvoreni skup \(\{1, 2\}\) u \(Y\) ima inverznu sliku \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), koja je takođe otvorena u \(X\).

Pošto je inverzna slika svakog otvorenog skupa iz \(Y\) otvoreni skup u \(X\), funkcija \(f\) je neprekidna.

Napomena: Prazan skup se ne razmatra jer je po definiciji otvoren u svakom topološkom prostoru.

Sada razmotrimo drugu funkciju \(g : X \to Y\), definisanu ovako:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

I ovu funkciju možemo prikazati dijagramom sa označenim otvorenim skupovima.

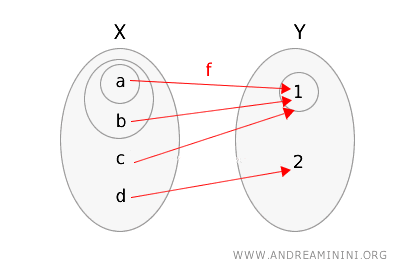
Provjerimo neprekidnost:

• Otvoreni skup \(\{1\}\) u \(Y\) ima inverznu sliku \(g^{-1}(\{1\}) = \{a, b, c\}\), koja nije otvorena u \(X\).

Pošto postoji otvoreni skup u \(Y\) čija inverzna slika nije otvorena u \(X\), funkcija \(g\) nije neprekidna.

Napomena: Ukratko, funkcija je neprekidna ako je inverzna slika svakog otvorenog skupa ciljnog prostora (\(Y\)) otvoreni skup u polaznom prostoru (\(X\)). U prvom primjeru funkcija \(f\) jeste neprekidna jer taj uslov uvijek važi, dok u drugom primjeru funkcija \(g\) nije, jer ga ne ispunjava za sve otvorene skupove.

Definicija homeomorfizma

Neka su \( X \) i \( Y \) topološki prostori, a \( f : X \to Y \) bijektivna funkcija koja ima inverznu funkciju \( f^{-1} : Y \to X \). Ako su i \( f \) i \( f^{-1} \) neprekidne, kažemo da je \( f \) homeomorfizam, a prostori \( X \) i \( Y \) su homeomorfni, odnosno \( X \cong Y \).

Takvi prostori se nazivaju i topološki ekvivalentni.

Šta to znači u praksi?

Dva prostora su homeomorfna, odnosno topološki ekvivalentna, ako dijele istu osnovnu topološku strukturu, čak i kada se njihovi geometrijski oblici bitno razlikuju.

Homeomorfizam se prepoznaje po tri osnovne osobine:

1. Bijektivnost: Funkcija \( f : X \to Y \) je istovremeno injektivna i surjektivna. Svaka tačka iz \( X \) odgovara tačno jednoj tački iz \( Y \), i obrnuto.
2. Neprekidnost funkcije \( f \): Funkcija je neprekidna ako je inverzna slika svakog otvorenog skupa iz \( Y \) otvoreni skup u \( X \).
3. Neprekidnost funkcije \( f^{-1} \): Inverzna funkcija \( f^{-1} : Y \to X \) mora takođe biti neprekidna, što znači da je inverzna slika svakog otvorenog skupa iz \( X \) otvoreni skup u \( Y \).

Primjer: Zamislite list papira koji se urola u cilindar. Cilindar i ravan list su homeomorfni jer se jedan može pretvoriti u drugi bez sječenja ili lijepljenja - dovoljno ga je zarolati ili odmotati. Iako im se geometrijski oblici razlikuju, njihova topološka struktura (odnosno otvoreni skupovi) ostaje ista.

Važno je naglasiti da činjenica da je bijektivna funkcija \( f \) neprekidna ne garantuje da je i njena inverzna funkcija \( f^{-1} \) neprekidna, osim ako je \( f \) ujedno i otvorena funkcija.

Drugim riječima, neprekidna i bijektivna funkcija nije nužno homeomorfizam ako njena inverzna funkcija nije neprekidna.

U topologiji kažemo da je funkcija \( f : X \to Y \) neprekidna kada je inverzna slika svakog otvorenog skupa iz \( Y \) otvoreni skup u \( X \).

To, međutim, ne znači da je direktna slika otvorenog skupa iz \( X \) nužno otvorena u \( Y \).

Da bi \( f^{-1} \) bila neprekidna, potrebno je da \( f \) bude ne samo neprekidna i bijektivna, već i otvorena funkcija.

Primjer

Razmotrimo sljedeće topološke prostore:

• \( X = (a, b) \) s topologijom \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) s topologijom \( T_Y = \{\emptyset, Y\} \).

Definišimo funkciju \( f : X \to Y \) tako da \( f(a) = 1 \) i \( f(b) = 2 \).

Ova funkcija je očigledno bijektivna: svakom elementu prostora \( X \) odgovara tačno jedan element prostora \( Y \), i obrnuto.

Napomena: Na dijagramu su otvoreni skupovi prikazani kružnicama. U prostoru \( X \) skupovi \{a\}, \{b\} i \{a, b\} su otvoreni, dok je u prostoru \( Y \) jedini otvoreni skup \{1, 2\}. Prazni skup, koji je po definiciji uvijek otvoren, ovdje nije prikazan.

Analizirajmo sada neprekidnost funkcije \( f \) i njenog inverza \( f^{-1} \).

• Neprekidnost funkcije \( f \)
  Topologija \( T_Y \) sadrži samo skupove \( \emptyset \) i \( Y \). Dakle:
  • \( f^{-1}(\emptyset) = \emptyset \), što je otvoren skup u \( T_X \).
  • \( f^{-1}(Y) = X \), takođe otvoren skup u \( T_X \).
  Dakle, funkcija \( f \) je neprekidna.
• Neprekidnost funkcije \( f^{-1} \)
  Razmotrimo sada \( f^{-1} : Y \to X \), pri čemu je \( f^{-1}(1) = a \) i \( f^{-1}(2) = b \). Otvoreni skupovi u \( X \) su:
  • \( f^{-1}(\emptyset) = \emptyset \), otvoren u \( T_Y \).
  • \( f^{-1}(\{a\}) = \{1\} \), koji nije otvoren u \( T_Y \).
  • \( f^{-1}(\{b\}) = \{2\} \), takođe nije otvoren u \( T_Y \).
  • \( f^{-1}(X) = Y \), otvoren u \( T_Y \).
  Budući da neke inverzne slike nisu otvorene, funkcija \( f^{-1} \) nije neprekidna.

Možemo zaključiti da, iako je \( f \) bijektivna i neprekidna, njen inverz to nije. Stoga \( f \) nije homeomorfizam.

Ovaj primjer jasno pokazuje da bijektivnost i neprekidnost same po sebi ne garantuju da će i inverzna funkcija biti neprekidna.

Napomena: Diskontinuitet funkcije \( f^{-1} \) rezultat je razlike u topologijama: topologija na \( X \) je finija (sadrži više otvorenih skupova) od one na \( Y \), koja je grublja.

Primjer 2

Razmotrimo sada drugi slučaj, sa drugačijim topologijama:

• \( X = (a, b) \) s topologijom \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) s topologijom \( T_Y = \{\emptyset, \{1\}, Y\} \).

Definišimo funkciju \( f : X \to Y \) tako da \( f(a) = 1 \) i \( f(b) = 2 \).

Funkcija \( f \) je ponovo bijektivna.

Provjerimo sada da li su \( f \) i \( f^{-1} \) neprekidne.

• Neprekidnost funkcije \( f \)
  Otvoreni skupovi u \( Y \) su \( \emptyset \), \(\{1\}\) i \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), otvoren u \( T_X \).
  • \( f^{-1}(\{1\}) = \{a\} \), otvoren u \( T_X \).
  • \( f^{-1}(Y) = X \), otvoren u \( T_X \).
  Sve inverzne slike su otvorene, pa je funkcija \( f \) neprekidna.
• Neprekidnost funkcije \( f^{-1} \)
  Otvoreni skupovi u \( X \) su \( \emptyset \), \(\{a\}\) i \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), otvoren u \( T_Y \).
  • \( f^{-1}(\{a\}) = \{1\} \), otvoren u \( T_Y \).
  • \( f^{-1}(X) = Y \), otvoren u \( T_Y \).
  Dakle, i inverzna funkcija \( f^{-1} \) je neprekidna.

Iz toga sledi da je \( f \) bijektivna, neprekidna, i da je njen inverz takođe neprekidan. Dakle, \( f \) je homeomorfizam.

Razlika u odnosu na prvi primjer ogleda se u tome što su ovdje topologije na \( X \) i \( Y \) usklađene tako da omogućavaju obostranu neprekidnost.

Napomena: Ovaj primjer pokazuje da, da bi postojala neprekidnost inverza i time i homeomorfizam, topologije na \( X \) i \( Y \) moraju biti međusobno kompatibilne.

Razlika između homeomorfizama i drugih topoloških transformacija

Iako se pojam „homeomorfizam" ponekad koristi u širem smislu za označavanje svih topoloških transformacija, on zapravo označava specifičnu i strogo definisanu vrstu preslikavanja.

Homeomorfizmi i topološke transformacije su blisko povezani, ali se ne poklapaju u potpunosti:

• Topološke transformacije
  Ovaj pojam obuhvata široku klasu preslikavanja između topoloških prostora koja čuvaju osnovna svojstva poput neprekidnosti, povezanosti ili kompaktosti. U ovu grupu spadaju ne samo homeomorfizmi, već i druge važne transformacije poput izotopija, homotopija i difeomorfizama.
• Homeomorfizmi
  To su preslikavanja koja su bijektivna i neprekidna, a čiji je inverz takođe neprekidan. Ona uspostavljaju potpunu topološku ekvivalenciju između dva prostora, čuvajući njihovu unutrašnju strukturu nepromijenjenom, iako im se geometrijski oblici mogu znatno razlikovati.

Ukratko, svaki homeomorfizam je topološka transformacija, ali ne svaka topološka transformacija mora biti homeomorfizam.

Pojedine funkcije, iako čuvaju neka bitna topološka svojstva, ne ispunjavaju sve uslove potrebne da bi bile homeomorfizmi i zato pripadaju širem, ali manje restriktivnom skupu transformacija.

Dodatna pojašnjenja

Za dublje razumijevanje značaja i primjene homeomorfizama korisno je istaći nekoliko važnih činjenica:

• Topološko svojstvo
  Topološko svojstvo je unutrašnja karakteristika prostora koja ostaje nepromijenjena pod djelovanjem homeomorfizma. Drugim riječima, ako su dva prostora homeomorfna (povezana bijektivnom i neprekidnom funkcijom čiji je inverz takođe neprekidan), ona dijele ista topološka svojstva.
• Hausdorffov teorem o homeomorfizmima
  Ovaj teorem tvrdi da ako je \( f : X \to Y \) homeomorfizam i ako je \( X \) Hausdorffov prostor, tada je i \( Y \) Hausdorffov. Pošto homeomorfizmi čuvaju topološka svojstva, svojstvo razdvajanja tačaka (karakteristično za Hausdorffove prostore) prenosi se sa \( X \) na \( Y \).
• Analogon homeomorfizma u algebri je izomorfizam grupa. Dok izomorfizam čuva algebarsku strukturu objekta, homeomorfizam čuva njegovu topološku strukturu, odnosno raspored otvorenih skupova unutar prostora.

I tako dalje.