Adherencija skupa
Adherencija skupa \( A \) u topološkom prostoru \( X \) definira se kao presjek svih zatvorenih skupova koji sadrže \( A \). Taj se presjek označava s \( \text{Cl}(A) \).
Jednostavno rečeno, adherencija skupa \( A \) predstavlja najmanji zatvoreni skup koji u potpunosti obuhvaća \( A \).
Drugim riječima, ne postoji nijedan zatvoreni skup koji sadrži \( A \), a da je strogo manji od njegove adherencije.
Napomena : Ovo svojstvo izravno proizlazi iz definicije. Budući da je adherencija definirana kao presjek svih zatvorenih skupova koji sadrže \( A \), ona automatski mora biti najmanji takav skup. Sastoji se upravo od onih elemenata koji pripadaju svim tim zatvorenim skupovima.
Formalna definicija adherencije glasi:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ i } C \text{ je zatvoren u } X \} $$
Ovdje \( \text{Cl}(A) \) označava adherenciju skupa \( A \), dok simbol \( \bigcap \) označava presjek svih zatvorenih skupova \( C \) koji sadrže \( A \).
Adherencija skupa \( A \) obuhvaća ne samo elemente samog skupa \( A \), nego i sve njegove točke akumulacije u prostoru \( X \).
Napomena : Važno je imati na umu da adherencija skupa prvenstveno ovisi o topologiji prostora u kojem se skup promatra, a ne o unutarnjim svojstvima skupa \( A \). Promjenom topologije može se promijeniti i njegova adherencija.
Ilustrativni primjer
Razmotrimo skup \( A = (0, 1) \) u skupu \( \mathbb{R} \), opremljenom standardnom topologijom.
Riječ je o otvorenom intervalu koji sadrži sve realne brojeve strogo između 0 i 1, bez uključivanja krajnjih točaka.
U tom slučaju adherencija skupa \( A \) jednaka je skupu \( [0,1] \).
$$ \text{Cl}(A) = [0,1] $$
Taj skup sadrži izvorni interval \( (0,1) \) kao i njegove točke akumulacije, odnosno krajnje točke 0 i 1.
Napomena : U standardnoj topologiji na \( \mathbb{R} \), skup je zatvoren ako sadrži sve svoje točke akumulacije. Točka je točka akumulacije ako u svakoj njezinoj okolini postoji barem jedna druga točka tog skupa. Na primjer, presjek zatvorenih intervala [0,2] i [-1,1] jednak je [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Ne postoji manji zatvoreni interval koji sadrži \( (0,1) \).
Primjer 2
Promotrimo sada skup \( A = [0, 1) \) u \( \mathbb{R} \), također u standardnoj topologiji.
Riječ je o intervalu koji je zatvoren s lij/hr/math/monotono-svojstvo-operatora-zatvaranjaeve strane i otvoren s desne, a sadrži sve realne brojeve od 0 uključivo do 1 isključivo.
I u ovom slučaju adherencija skupa iznosi \( [0,1] \).
$$ \text{Cl}(A) = [0,1] $$
Točka 0 već pripada skupu \( A \), dok je točka 1 točka akumulacije koja ne pripada samom skupu.
Zbog toga adherencija skupa mora uključivati i desnu krajnju točku, čime nastaje zatvoreni skup \( [0,1] \), najmanji mogući koji sadrži \( A \).
Napomena : Ovaj primjer jasno pokazuje kako definicija adherencije nužno uključuje sve točke akumulacije. Kao i ranije, vrijedi $$ [0,2] \cap [-1,1]=[0,1] $$
Primjer 3
Razmotrimo isti skup \( A = [0,1) \), ali sada u prostoru \( X \) opremljenom diskretnom topologijom.
U diskretnoj topologiji svaki je podskup prostora istodobno otvoren i zatvoren.
- Otvoren skup
Svaki podskup skupa \( X \) je otvoren, pa je i \( A \) otvoren skup. - Zatvoren skup
Budući da je komplement svakog podskupa otvoren, svaki je podskup ujedno i zatvoren. Stoga je i \( A \) zatvoren.
Takvi se skupovi nazivaju clopen skupovi, jer su istodobno otvoreni i zatvoreni.
Kako je \( A \) već zatvoren, njegova adherencija se podudara s njim samim.
$$ \text{Cl}(A) = [0,1) $$
Najmanji zatvoreni skup koji sadrži \( A \) u ovom slučaju jest upravo \( A \).
Napomena : Ovaj primjer jasno pokazuje koliko izbor topologije može utjecati na adherenciju skupa.
Primjer 4
Razmotrimo topološki prostor \( X = \{a, b, c\} \), opremljen diskretnom topologijom.
U tom prostoru svaki je podskup otvoren, a time i zatvoren:
- Skupovi \( \emptyset \) i \( \{a, b, c\} \) otvoreni su po definiciji.
- Jednočlani skupovi \( \{a\} \), \( \{b\} \) i \( \{c\} \) također su otvoreni.
- Svi njihovi podskupovi, poput \( \{a, b\} \), \( \{a, c\} \) i \( \{b, c\} \), također su otvoreni.
Budući da su svi skupovi zatvoreni, adherencija bilo kojeg skupa jednaka je tom skupu.
Ako uzmemo \( A = \{b, c\} \), tada vrijedi:
\[ \text{Cl}(A) = \{b, c\} \]
Napomena : Zatvoreni skupovi koji sadrže \( A \) su \( \{b, c\} \) i \( \{a, b, c\} \). Njihov presjek daje $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ pa se adherencija u diskretnoj topologiji uvijek poklapa s izvornim skupom.
Teorem o adherenciji skupa
U topološkom prostoru \( X \), točka \( y \) pripada adherenciji podskupa \( S \), označenoj s \( \text{Cl}(S) \), ako i samo ako svaki otvoreni skup \( U \) koji sadrži \( y \) ima neprazan presjek sa \( S \) : \( y \in \text{Cl}(S) \iff \forall \ U \text{ otvoren takav da } y \in U,\ U \cap S \neq \emptyset \).
Intuitivno, to znači da se točka \( y \) nalazi u adherenciji skupa \( S \) ako se nijednom otvorenom okolinom oko \( y \) ne može „izbjeći" skup \( S \).
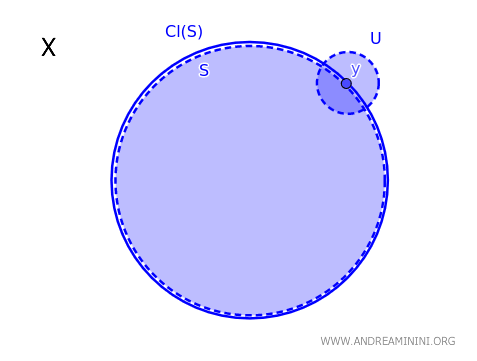
Ovaj teorem daje jasan i praktičan kriterij za provjeru pripada li neka točka adherenciji određenog skupa u topološkom prostoru.
Dokaz
- Nužni uvjet : Ako vrijedi \( y \in \text{Cl}(S) \), tada po definiciji svaki otvoreni skup koji sadrži \( y \) mora presijecati skup \( S \). Razlog je u tome što adherencija obuhvaća kako elemente skupa \( S \), tako i njegove točke akumulacije. Točka akumulacije jest točka čija svaka okolina sadrži barem jednu točku skupa \( S \).
- Dovoljni uvjet : Obrnuto, ako svaki otvoreni skup koji sadrži \( y \) ima neprazan presjek sa \( S \), tada je \( y \) ili element skupa \( S \), ili njegova točka akumulacije. U oba slučaja slijedi da \( y \in \text{Cl}(S) \), jer ne postoji otvorena okolina točke \( y \) koja je disjunktna od skupa \( S \).
Napomena : Teorem o adherenciji jedan je od temeljnih rezultata opće topologije. On povezuje pojam otvorenih skupova s graničnim ponašanjem skupova te se često koristi u proučavanju kontinuiteta funkcija, konvergencije nizova i mreža, kao i u brojnim klasičnim dokazima.
Primjer
Razmotrimo skup \( A = (0, 2) \), opremljen standardnom topologijom na \( \mathbb{R} \), odnosno otvoreni interval realnih brojeva.
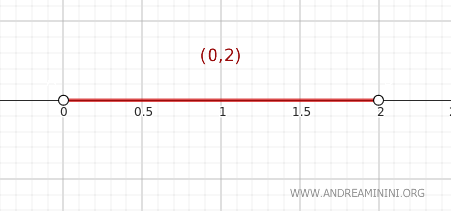
Primijenimo teorem kako bismo utvrdili pripada li točka \( y \) adherenciji skupa \( A \).
Odaberimo točku \( y = 2 \in \mathbb{R} \).
Prema teoremu, vrijedi da je \( y \in \text{Cl}(A) \) ako i samo ako svaki otvoreni skup koji sadrži \( y \) ima neprazan presjek sa \( A \).
- Analiza okolina točke \( y \) : Svaki otvoreni interval koji sadrži \( y = 2 \), primjerice \( (1{,}9, 2{,}1) \), \( (1{,}95, 2{,}05) \) ili \( (1{,}99, 2{,}01) \), nužno sadrži točke skupa \( A = (0, 2) \), poput \( 1{,}95 \) ili \( 1{,}99 \).
- Zaključak : Budući da svaka otvorena okolina točke \( y = 2 \) sadrži barem jednu točku skupa \( A \), slijedi da \( y = 2 \) pripada adherenciji skupa \( A \).
Prema tome, točka \( y = 2 \) pripada adherenciji skupa \( A \).
$$ y \in \text{Cl}(A) $$
Iz toga zaključujemo da je adherencija skupa \( A \) zatvoreni interval \( \text{Cl}(A) = [0, 2] \), koji uključuje i krajnju točku \( 2 \).
Svojstva adherencije u topološkim prostorima
U nastavku su navedena neka osnovna svojstva adherencije u topološkim prostorima, zajedno s njihovim odnosima prema pojmu unutrašnjosti, koji su često na prvi pogled neintuitivni.
- Unutrašnjost komplementa i komplement adherencije
Unutrašnjost komplementa skupa \( A \) jednaka je komplementu njegove adherencije: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$ - Adherencija komplementa i komplement unutrašnjosti
Adherencija komplementa skupa \( A \) podudara se s komplementom njegove unutrašnjosti: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$
Bitne napomene
Sljedeća svojstva dodatno pojašnjavaju ulogu adherencije u topologiji:
- Ako je \( C \) zatvoren skup u \( X \) i \( A \subseteq C \), tada vrijedi \( \text{Cl}(A) \subseteq C \)
Budući da je \( \text{Cl}(A) \) najmanji zatvoreni skup koji sadrži \( A \), on je nužno sadržan u svakom zatvorenom skupu koji sadrži \( A \). - Ako je \( A \subseteq B \), tada vrijedi \( \text{Cl}(A) \subseteq \text{Cl}(B) \)
Adherencija je monotona operacija: uključenje skupova povlači uključenje njihovih adherencija. - Skup \( A \) je zatvoren ako i samo ako vrijedi \( A = \text{Cl}(A) \)
Ovo svojstvo daje temeljnu karakterizaciju zatvorenih skupova u topologiji. - Adherencija skupa jednaka je uniji skupa i njegovih točaka akumulacije
Ako je \( A' \) skup svih točaka akumulacije skupa \( A \), tada vrijedi: $$ \text{Cl}(A) = A \cup A' $$ - Idempotentnost
Ponovna primjena operacije adherencije ne mijenja rezultat: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - Uključenje izvornog skupa
Svaki skup sadržan je u vlastitoj adherenciji: $$ A \subseteq \text{Cl}(A) $$
Dodatni povezani sadržaji bit će dostupni uskoro.