Regularni topološki prostori
Topološki prostor \( X \) naziva se regularnim ako ispunjava dva osnovna uslova:
- Singltoni su zatvoreni: svaka tačka u prostoru formira zatvoren skup.
- Možemo razdvojiti tačku od zatvorenog skupa: za tačku \( a \in X \) i zatvoren skup \( C \subseteq X \) koji je ne sadrži, postoje dva otvorena skupa \( U \) i \( V \) takva da: \[ a \in U, \quad C \subseteq V, \quad U \cap V = \emptyset. \]
Regularni prostori imaju jača svojstva razdvajanja od Hausdorffovih prostora, što ih čini važnim u izučavanju strukture topoloških prostora. Kada prostor ima i prebrojivu bazu, Urysohnov teorem garantuje da ga je moguće metrizarati, što otvara vrata mnogim rezultatima analize.
Regularni naspram Hausdorffovih prostora
Ključna razlika je jednostavna: Hausdorffov prostor razdvaja tačke, dok regularni prostor ide korak dalje i omogućava razdvajanje tačke od zatvorenog skupa koji je ne sadrži. Ovo dodatno svojstvo čini regularnost jačim oblikom razdvajanja.
Napomena. Regularnost ne garantuje normalnost. Normalni prostori zahtijevaju da se mogu razdvojiti svaki par disjunktnih zatvorenih skupova. Svaki normalan prostor jeste regularan, ali postoji mnogo regularnih prostora koji nisu normalni.
Regularnost je samo jedan od aksioma razdvajanja. Mnogi prostori zadovoljavaju neke, ali ne sve ove aksiome, što daje veoma raznoliku i bogatu sliku topoloških struktura.
Primjer: realna prava kao regularan prostor
Realna prava \( \mathbb{R} \) sa standardnom topologijom često služi kao ilustracija osnovnih topoloških svojstava, pa tako i regularnosti.
Uzmimo tačku \( x = 2 \) i zatvoren skup:
\[ C = (-\infty, 0] \cup [5, \infty). \]
Tačka 2 očigledno nije u skupu \( C \), pa možemo ispitati kako ih odvojiti otvorenim skupovima.

Komplement skupa \( C \) je otvoren i sadrži interval \( (0, 5) \), u kojem se nalazi vrijednost 2. Unutar tog intervala biramo brojeve \( c \) i \( d \) takve da:
\[ 0 < c < 2 < d < 5. \]
Na primjer, biramo \( c = 1 \) i \( d = 3 \). Time dobijamo dva otvorena skupa:
- \( U = (1, 3) \), koji obuhvata tačku \( x = 2 \).
- \( V = (-\infty, 1) \cup (3, \infty) \), koji obuhvata zatvoreni skup \( C \).
Ova dva skupa su potpuno odvojena, jer je njihov presjek prazan. Upravo to razdvajanje pokazuje regularnost realne prave.
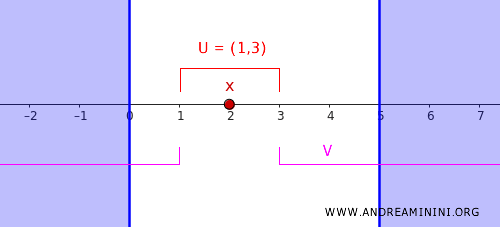
Primjer jasno pokazuje da u regularnom prostoru možemo pronaći otvorene okoline koje razdvajaju strukture koje ne smiju biti u dodiru.
Bilješke
Za dublje razumijevanje regularnih prostora korisno je imati na umu nekoliko ideja:
- Aksiomi razdvajanja čine osnovu teorije topoloških prostora. Oznake poput T2 (Hausdorffov), T3 (regularan) i T4 (normalan) određuju koliko fino prostor može razlikovati svoje elemente.
Napomena. Hausdorffov prostor razdvaja tačke, a regularan prostor razdvaja tačku i zatvoren skup. Ove razlike određuju koliko je precizna struktura prostora, gotovo poput rezolucije slike: što je veća, to je slika jasnija.
Ovi koncepti predstavljaju temelj za dublja istraživanja u topologiji i pomažu u razumijevanju kako različiti prostori funkcionišu, razvijaju se i međusobno razlikuju.