Hausdorffov prostor

Hausdorffov prostor je topološki prostor u kojem se svaka dvije različite tačke mogu razdvojiti pomoću otvorenih skupova koji se međusobno ne preklapaju. To znači da svaka tačka ima dovoljno “prostora oko sebe” da je možemo jasno razlikovati od ostalih.

Formalno, za svako \( x \ne y \) postoje otvoreni skupovi \( U \) i \( V \) takvi da \( x \in U \), \( y \in V \) i \( U \cap V = \emptyset \).

Ovakvo svojstvo daje preciznu matematičku verziju ideje iz euklidske geometrije. Ako su dvije tačke različite, možemo ih odvojiti tako da svaka ima svoje otvoreno okruženje koje se ne sudara s drugim.

Hausdorffovi prostori važni su u analizi i geometriji jer omogućavaju jasnu i pouzdanu teoriju konvergencije. U takvim prostorima granica konvergentnog niza uvijek je jedinstvena, što je ključno za mnoge matematičke konstrukcije.

Jedan od osnovnih rezultata glasi da su u svakom Hausdorffovom prostoru singletoni zatvoreni skupovi.

Zašto? Komplement tačke je uvijek otvoren, pa tačka sama po sebi mora biti zatvorena.

Primjeri

Primjer 1

Uzmimo standardnu topologiju na realnoj pravoj \(\mathbb{R}\), zasnovanu na otvorenim intervalima.

U ovoj topologiji singleton \( \{x\} \) nije otvoren skup.

Zašto? Otvoren skup mora sadržati neko otvoreno okruženje svake svoje tačke. Singleton nema širinu i ne može obuhvatiti otvoreni interval oko \( x \) bez hvatanja dodatnih tačaka. Zato nije otvoren.

S druge strane, komplement \( \mathbb{R} \setminus \{x\} \) jeste otvoren.

Time je jasno da je \( \{x\} \) zatvoren skup.

Realna prava sa svojom uobičajenom topologijom takođe je Hausdorffov prostor. Za svako \( a \ne b \) možemo pronaći otvorene intervale koji ih razdvajaju.

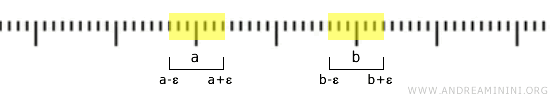
Ako je \( a < b \), izaberemo \( \varepsilon > 0 \) tako da \( a + \varepsilon < b - \varepsilon \). Tada su intervali \( (a - \varepsilon, a + \varepsilon) \) i \( (b - \varepsilon, b + \varepsilon) \) disjunktni.

Primjer 2

Razmotrimo konačan skup \( X = \{1, 2, 3\} \) s diskretnom topologijom.

U diskretnoj topologiji svaki singleton je otvoren po definiciji, pa su otvoreni svi podskupovi skupa \( X \):

• prazan skup \( \emptyset \)
• singletoni \( \{1\}, \{2\}, \{3\} \)
• parovi \( \{1, 2\}, \{1, 3\}, \{2, 3\} \)
• cijeli skup \( \{1, 2, 3\} \)

Ukupno ih je \( 2^3 = 8 \), koliko ima i svih podskupova.

U ovakvom prostoru \( X \) je automatski Hausdorffov prostor, jer za svaki par \( x \ne y \) možemo uzeti jednostavna, disjunktna otvorena okruženja \( \{x\} \) i \( \{y\} \).

To dobro ilustruje glavnu razliku između diskretne i standardne topologije: u diskretnoj topologiji svi podskupovi su otvoreni, dok u standardnoj samo neki od njih mogu biti otvoreni.

Napomene

Evo jedne od najvažnijih posljedica Hausdorffovog svojstva:

• Svaki konvergentni niz u Hausdorffovom prostoru ima jedinstvenu granicu.
  Drugim riječima, niz ne može konvergirati prema dvjema različitim tačkama. Kada bi to bilo moguće, te dve tačke mogle bi se razdvojiti disjunktnim otvorenim okruženjima, što je u suprotnosti s konceptom konvergencije.

Dokaz (skica): Pretpostavimo da niz \( x_1, x_2, x_3, \dots \) istovremeno konvergira ka \( x \) i ka \( y \) u Hausdorffovom prostoru. Po definiciji, za svako otvoreno okruženje \( U \) tačke \( x \) postoji \( N \) takav da su svi članovi niza od nekog mjesta nadalje u \( U \). Isto važi za \( y \) i njegovo okruženje \( V \).

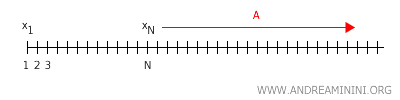
Ali ako su \( x \ne y \), Hausdorffovo svojstvo garantuje postojanje disjunktnih okruženja \( U \) i \( V \). To bi značilo da su termini niza istovremeno u oba okruženja, što je nemoguće.

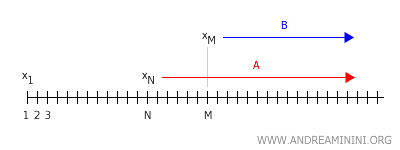
Zato konvergentan niz u Hausdorffovom prostoru može imati samo jednu granicu. Jedinstvenost je zagarantovana samom strukturom prostora.