Clopen skupovi

Skup nazivamo clopen ako je u istoj topologiji istovremeno otvoren i zatvoren.

Takvi skupovi predstavljaju zanimljiv pojam u topologiji jer spajaju dva naizgled suprotna svojstva. Otvoreni skupovi intuitivno opisuju područja bez rubova, dok zatvoreni skupovi uključuju svoje granice. Clopen skupovi pripadaju objema kategorijama u isto vrijeme, što ih čini korisnima u analizi strukture topoloških prostora.

Naziv clopen nastao je kombinacijom engleskih riječi closed i open. Ti skupovi istodobno imaju obilježja svojstvena i otvorenim skupovima i zatvorenim skupovima.

Clopen situacija nastaje kada su neki skup i njegov komplement oba otvorena u istoj topologiji.

Napomena: U skupu realnih brojeva clopen skupovi javljaju se samo u trivijalnim slučajevima, ali u drugim topološkim prostorima mogu biti ključni za razumijevanje logike prostora. Zato imaju važnu ulogu u proučavanju topoloških struktura.

Primjer iz diskretne topologije

Promotrimo skup \(X=\{a,b,c,d\}\) s topologijom \(T\).

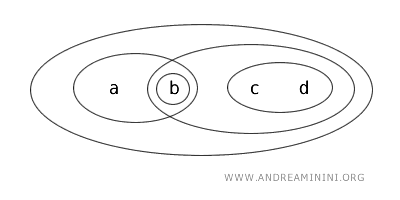
Otvoreni skupovi u topologiji \(T\) su: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).

Iz toga slijedi da je \(\{a,b\}\) otvoren skup u \(T\).

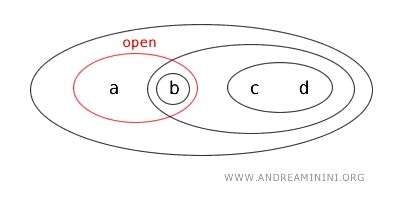
Istodobno, \(\{a,b\}\) je komplement otvorenog skupa \(\{c,d\}\):

$$ X - \{ c,d \} = \{a , b \} $$

Budući da je komplement otvorenog skupa uvijek zatvoren skup:

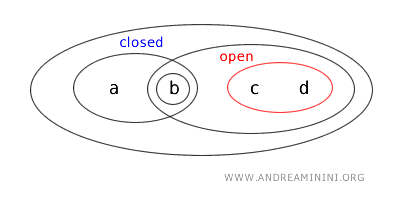
možemo zaključiti da je \(\{a,b\}\) i zatvoren skup. Dakle, u topologiji \(T\) ovaj skup istovremeno je otvoren i zatvoren, pa je clopen.

Zašto su prazan i cijeli skup uvijek clopen

U svakoj topologiji nad skupom \(X\), prazan skup (\(\varnothing\)) i cijeli skup (\(X\)) uvijek su clopen jer zadovoljavaju obje definicije.

Prazan i cijeli skup polazišna su točka svake topologije i prirodno ispunjavaju tražene uvjete. Prazan skup otvoren je po aksiomima, a zatvoren jer mu je komplement cijeli skup. Cijeli skup otvoren je po definiciji, a zatvoren jer mu je komplement prazan skup.

• Prazan skup (\(\varnothing\))
  Otvoren je prema topološkim aksiomima. Komplement mu je \(X\), koji je također otvoren, pa je istodobno i zatvoren.
• Cijeli skup (\(X\))
  Otvoren je po definiciji. Budući da je njegov komplement \(\varnothing\), a on je otvoren, cijeli skup također je zatvoren.

Zaključno, u svakoj topologiji prazan skup i cijeli skup čine osnovne primjere clopen skupova. Ovaj koncept, iako na prvi pogled jednostavan, otkriva važan uvid u strukturu prostora i način na koji se topološki skupovi mogu međusobno povezivati.

I tako dalje.