Skupovi koji nisu ni otvoreni ni zatvoreni
U topologiji postoji posebna kategorija skupova koji nisu ni otvoreni ni zatvoreni. Oni jednostavno ne ispunjavaju uslove potrebne da bi bili svrstani u jednu od ove dvije jasno definisane grupe.
Do ovakvih situacija dolazi kada posmatrani skup nije definisan kao otvoreni skup niti kao komplement nekog otvorenog skupa. Zbog toga ga ne možemo smatrati ni zatvorenim skupom.
Napomena: U standardnoj topologiji skupa realnih brojeva ovi slučajevi se rijetko pominju i mogu djelovati neobično. Ipak, u širim topološkim prostorima potpuno su prirodni i često se javljaju. Kratak primjer pomoći će da se ideja odmah razjasni.
Primjer
Posmatrajmo skup \( X = \{a,b,c,d\} \) i topologiju \( T \) određenu sljedećim otvorenim skupovima: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) i praznim skupom (Ø).
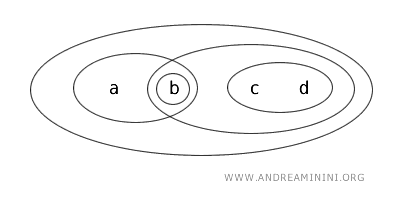
Posmatrajmo sada podskup \( \{b,c\} \) skupa \( X \).
- Skup \( \{b,c\} \) nije otvoren u topologiji \( T \), jer se ne nalazi među navedenim otvorenim skupovima.
- Istovremeno, \( \{b,c\} \) nije zatvoren, zato što njegov komplement \( X \setminus \{b,c\} = \{a,d\} \) ne pripada zbirci otvorenih skupova u \( T \).
Zaključak je jasan. U topologiji \( T \), podskup \( \{b,c\} \) ne može biti svrstan ni među otvorene ni među zatvorene skupove. Ovakvi primjeri podsjećaju nas da topologija obuhvata mnogo širu sliku od one na koju smo navikli u kontekstu realnih brojeva.
I tako dalje.