Fiksne točke u topologiji
U topologiji, fiksna točka je vrijednost koja ostaje ista nakon primjene funkcije. Drugim riječima, sustav je u toj točki stabilan jer se ne mijenja pod djelovanjem preslikavanja.
Promatramo li funkciju f(x), kažemo da je p fiksna točka ako vrijedi f(p) = p. Ulaz i izlaz potpuno se podudaraju.
$$ f(p) = p $$
Za intuitivan primjer, zamislite rotaciju nekog oblika oko središnje točke P. Sve ostale točke mijenjaju položaj, dok P ostaje nepomična u prostoru.
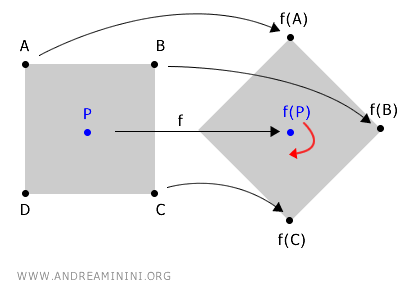
Zbog toga se P smatra fiksnom točkom. Neovisno o rotaciji, preslikavanje f(P) vraća istu koordinatu.
$$ f(P) \longrightarrow P $$
Fiksne točke imaju ključnu ulogu u mnogim granama matematike, ali i u stvarnim primjenama. Pojavljuju se u numeričkim metodama, analizi stabilnosti, teoriji igara, ekonomiji i dinamičkim sustavima. Jedan od najpoznatijih rezultata povezanih s ovim konceptom je Brouwerov teorem o fiksnoj točki.
Primjeri funkcija s fiksnim točkama
Razmotrimo funkciju f(x) = sin(x) na intervalu [0, 2π].
$$ f(x) = \sin(x) $$
Vidimo da je x = 0 fiksna točka jer vrijedi sin(0) = 0.
$$ \sin(0) = 0 $$
Drugi primjer
Sada promotrimo funkciju f(x) = cos(x) na istom intervalu.
$$ f(x) = \cos(x) $$
U ovom slučaju x = 0 nije fiksna točka jer cos(0) = 1. No funkcija ima fiksnu točku približno u x = 0.73908513 radijana.
$$ \cos(0.73908513) = 0.73908513 $$
Takve se vrijednosti često pronalaze numeričkim metodama, a njihov položaj nije uvijek očit na prvi pogled.
Brouwerov teorem o fiksnoj točki
Teorem navodi:
Svaka neprekinuta funkcija koja preslikava zatvoreni i ograničeni skup u n-dimenzionalnom prostoru ima najmanje jednu fiksnu točku.
Riječ je o teoremu koji jamči postojanje rješenja, ali ga ne mora eksplicitno odrediti. Upravo zbog toga Brouwerov rezultat ima snažan utjecaj u analizi sustava koji teže ravnoteži, bilo u fizici, biologiji, ekonomiji ili drugim znanostima.
Koncept fiksnih točaka otvara mnoge putove za daljnje istraživanje, a u naprednijim područjima povezuje se s iteracijama, stabilnošću i svojstvima preslikavanja. Ovo je tek polazište za dublje razumijevanje njihove uloge u matematici i primijenjenim znanostima.