Granica skupa

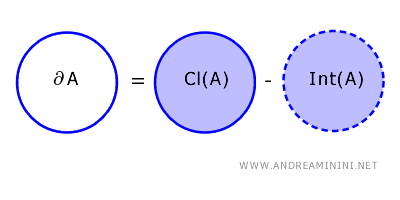
Granica podskupa $ A $ topološkog prostora $ X $ definiše se kao skup svih tačaka koje pripadaju zatvaranju skupa $ A $, ali ne pripadaju njegovoj unutrašnjosti : \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

Intuitivno, granica opisuje „prelaznu zonu“ između skupa i njegovog okruženja. To su tačke koje nisu jasno ni unutar skupa, ni potpuno izvan njega.

Ovdje $ \text{Cl}(A) $ označava zatvaranje skupa $ A $, koje obuhvata sve njegove tačke zajedno sa svim limesnim (graničnim) tačkama.

S druge strane, $ \text{Int}(A) $ predstavlja unutrašnjost skupa $ A $, odnosno skup tačaka za koje postoji neko okruženje u potpunosti sadržano u $ A $.

primjer granice skupa

Važno je naglasiti da pojam granice zavisi od izabrane topologije na prostoru $ X $. Zbog toga granica nije intrinzično svojstvo skupa, već zavisi od strukture prostora u kojem se skup posmatra.

Drugim riječima, jedan te isti skup može imati različitu granicu u različitim topologijama.

Granica skupa $ A $ sastoji se od onih tačaka koje su « bliske » i skupu $ A $ i njegovom komplementu $ X \setminus A $.

Konkretan primjer
Teorem o granici skupa
Napomene

Konkretan primjer

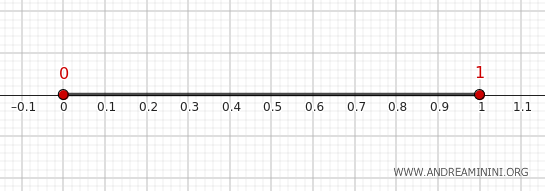
Razmotrimo skup $ A = (0, 1) $, posmatran kao podskup realne prave $ \mathbb{R} $ sa njenom uobičajenom topologijom.

Granicu ovog skupa odredićemo sistematski, kroz nekoliko jasnih koraka.

1] Zatvaranje skupa A

Zatvaranje skupa $ A $, označeno sa $ \text{Cl}(A) $, obuhvata sve tačke skupa $ A $ kao i sve njegove akumulacione (limesne) tačke.

Za skup $ A = (0, 1) $, zatvaranje je zatvoreni interval $[0, 1]$. Razlog je što su tačke 0 i 1 granične tačke skupa $ A $, dok su sve unutrašnje tačke već njegov dio.

$$ \text{Cl}(A) = [0, 1] $$

2] Unutrašnjost skupa A

Unutrašnjost skupa $ A $, označena sa $ \text{Int}(A) $, sastoji se od svih tačaka koje posjeduju neko okruženje potpuno sadržano u skupu $ A $.

Budući da je $ A = (0, 1) $ otvoreni interval, njegova unutrašnjost podudara se sa samim skupom:

$$ \text{Int}(A) = (0, 1) $$

3] Granica skupa A

Granica skupa $ A $, označena sa $ \partial A $, dobija se oduzimanjem unutrašnjosti od zatvaranja:

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

Uvrštavanjem prethodnih rezultata dobijamo:

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

Prema tome, u uobičajenoj topologiji na $ \mathbb{R} $, granicu skupa $ A = (0,1) $ čine upravo tačke $\{0, 1\}$.

Ove tačke se nalaze „na rubu“ skupa, jer svako njihovo okruženje sadrži istovremeno elemente skupa $ A $ i elemente njegovog komplementa $ X \setminus A $.

granica skupa na realnoj pravoj

Teorem o granici skupa

Tačka $ x \in X $ pripada granici $ \partial A $ podskupa $ A $ ako i samo ako svako njeno okruženje ima neprazan presjek i sa skupom $ A $ i sa njegovim komplementom $ X - A $.

Ovaj teorem pruža jasan i praktičan kriterij: da bismo utvrdili da li tačka $ x $ pripada granici skupa $ A $, dovoljno je provjeriti da svako njeno okruženje istovremeno presijeca i skup $ A $ i skup $ X - A $.

Primjer

Ponovo razmotrimo skup $ A = (0, 1) $ u prostoru $ \mathbb{R} $, opremljenom standardnom topologijom.

U tom slučaju vrijedi:

$$ \text{Cl}(A) = [0, 1] \quad \text{i} \quad \text{Int}(A) = (0, 1) $$

Iz toga neposredno slijedi da je granica skupa:

$$ \partial A = \{0, 1\} $$

Provjerimo sada, korak po korak, da li ove tačke zaista zadovoljavaju kriterij naveden u teoremu o granici.

1] Provjera za tačku 0

Razmotrimo proizvoljno okruženje tačke 0, na primjer otvoreni interval $ (0 - \epsilon, 0 + \epsilon) $, gdje je $ \epsilon > 0 $.

Ovo okruženje presijeca skup $ A $, jer sadrži tačke iz intervala $ (0, 1) $, ali istovremeno presijeca i skup $ X - A $, budući da sadrži tačke manje ili jednake od 0.

Prema kriteriju teorema, iz toga slijedi da tačka 0 pripada granici skupa, odnosno da je $ 0 \in \partial A $.

okruženje tačke 0

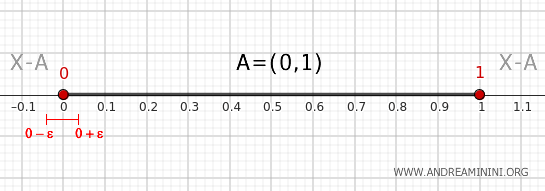
2] Provjera za tačku 1

Na isti način, razmotrimo okruženje tačke 1, na primjer interval $ (1 - \epsilon, 1 + \epsilon) $.

I ovo okruženje presijeca skup $ A $, jer sadrži tačke iz intervala $ (0,1) $, ali takođe presijeca i skup $ X - A $, jer uključuje tačke veće ili jednake od 1.

Prema tome, i tačka 1 ispunjava uslov teorema, pa vrijedi $ 1 \in \partial A $.

okruženje tačke 1

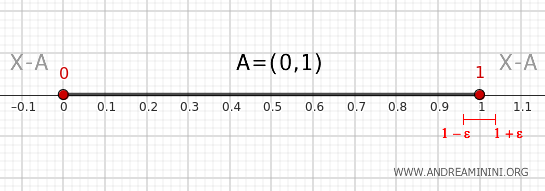
3] Provjera za unutrašnju tačku

Izaberimo sada proizvoljnu tačku iz intervala $ (0,1) $, na primjer 0,5.

Svako okruženje tačke 0,5 u potpunosti je sadržano u skupu $ A $. Zbog toga takvo okruženje ne može presijecati skup $ X - A $.

Otuda slijedi da tačka 0,5 ne pripada granici skupa, odnosno da vrijedi $ 0.5 \notin \partial A $.

okruženje tačke 0.5

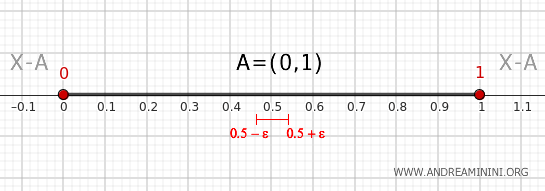
Ukratko, teorem jasno potvrđuje da tačke 0 i 1 pripadaju granici skupa $ A = (0, 1) $, dok unutrašnje tačke, poput 0,5, ne pripadaju granici. Prema tome, granica skupa je upravo $\{0, 1\}$.

Napomene

U nastavku navodimo neke važne i često korišćene osobine granice u topologiji:

Granica $ \partial A $ sadržana je u skupu $ A $ ako i samo ako je $ A $ zatvoren skup:
\[ \partial A \subseteq A \Leftrightarrow A \text{ je zatvoren} \]
Granica $ \partial A $ i skup $ A $ su disjunktni ako i samo ako je $ A $ otvoren:
Drugim riječima, skup $ A $ je otvoren ako i samo ako nijedna njegova tačka ne leži na njegovoj granici.
\[ \partial A \cap A = \emptyset \;\Leftrightarrow A \text{ je otvoren} \]
Granica $ \partial A $ je prazna ako i samo ako je $ A $ istovremeno otvoren i zatvoren (clopen):
\[ \partial A = \emptyset \Leftrightarrow A \text{ je clopen} \]
Granica $ \partial A $ jednaka je presjeku zatvaranja skupa $ A $ i zatvaranja njegovog komplementa $ X - A $:
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \]
Granica $ \partial A $ je uvijek zatvoren skup:

Presjek dva zatvorena skupa je zatvoren. Budući da je $ \partial A $ definisana kao $\text{Cl}(A) \cap \text{Cl}(X - A)$, neposredno slijedi da je granica svakog skupa uvijek zatvoren skup.
Granica i unutrašnjost skupa uvijek su disjunktne:
\[ \partial A \cap \text{Int}(A) = \emptyset \]
Unija unutrašnjosti i granice jednaka je zatvaranju skupa:
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]

I tako dalje.