Teorem o rubu skupa
Tačka \( x \) pripada rubu skupa \( A \) ako se u svakom njenom susedstvu nalaze i tačke skupa \( A \) i tačke njegovog komplementa \( X - A \).
Drugim rečima, tačka \( x \) je tačka ruba skupa \( A \) ako ne postoji nijedno njeno susedstvo koje je u potpunosti sadržano u skupu \( A \), niti nijedno koje je u potpunosti sadržano u njegovom komplementu.
Ilustrativan primer
Da bismo ovu definiciju učinili jasnijom, razmotrimo jednostavan i dobro poznat primer.
Neka je skup \( A = (0, 1) \) na realnoj pravoj \( \mathbb{R} \).
Tačke 0 i 1 čine rub skupa \( A \), jer svako njihovo susedstvo sadrži i tačke koje pripadaju intervalu \( (0, 1) \), ali i tačke koje se nalaze izvan tog intervala.
- Tačka 1
Svako susedstvo oblika \( (1 - \epsilon, 1 + \epsilon) \), gde je ε proizvoljno malo, sastoji se iz dva dela. Interval \( (1 - \epsilon, 1) \) pripada skupu \( A \), dok se interval \( (1, 1 + \epsilon) \) nalazi izvan skupa \( A \). Zbog toga je tačka 1 tačka ruba skupa \( A \).
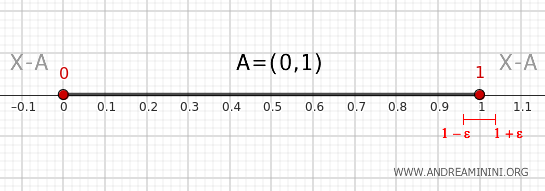
- Tačka 0
Analogno prethodnom slučaju, svako susedstvo \( (0 - \epsilon, 0 + \epsilon) \) sadrži deo \( (0, 0 + \epsilon) \) koji pripada skupu \( A \), kao i deo \( (0 - \epsilon, 0) \) koji pripada njegovom komplementu. Prema tome, i tačka 0 je tačka ruba skupa \( A \).
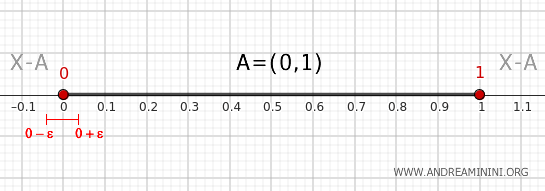
- Unutrašnja tačka intervala (0, 1)
Svaka tačka \( x \) za koju važi \( 0 < x < 1 \) ima susedstvo \( (x - \epsilon, x + \epsilon) \), sa ε > 0, koje je u celosti sadržano u skupu \( A \). Takvo susedstvo ne sadrži tačke komplementa, pa ove tačke ne pripadaju rubu skupa.
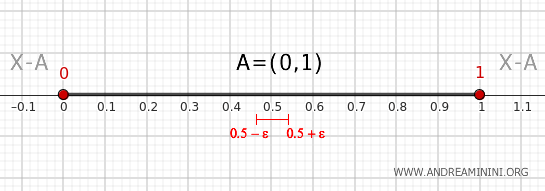
- Spoljašnja tačka u odnosu na interval (0, 1)
Svaka tačka koja se nalazi izvan intervala \( (0, 1) \), osim krajnjih tačaka 0 i 1, ima susedstvo koje je u potpunosti sadržano u skupu \( X - A \), bez preseka sa skupom \( A \). Zbog toga takve tačke ne pripadaju rubu skupa.
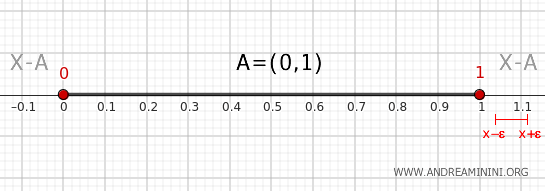
Iz prethodnih razmatranja zaključujemo da su jedine tačke ruba skupa \( A \) upravo tačke 0 i 1:
$$ \partial A = \{0,1 \} $$
U sažetom obliku, tačka pripada rubu skupa onda i samo onda kada nijedno njeno susedstvo ne može biti u potpunosti smešteno ni u sam skup, ni u njegov komplement. Ovaj kriterijum omogućava jasno i precizno prepoznavanje tačaka ruba.
Dokaz
Dokaz teorema zasniva se na razmatranju dve logičke implikacije.
1] Pretpostavimo da je \( x \in \partial A \)
Po definiciji ruba važi:
$$ x \in \text{Cl}(A) \quad \text{i} \quad x \notin \text{Int}(A) $$
Uslov \( x \in \text{Cl}(A) \) znači da svako susedstvo tačke \( x \) ima neprazan presek sa skupom \( A \).
Uslov \( x \notin \text{Int}(A) \) znači da nijedno susedstvo tačke \( x \) nije u potpunosti sadržano u skupu \( A \), pa svako susedstvo mora sadržati i tačke iz skupa \( X - A \).
Otuda sledi da svako susedstvo tačke \( x \) seče i skup \( A \) i njegov komplement.
2] Pretpostavimo da svako susedstvo tačke \( x \) seče i \( A \) i \( X - A \)
Iz ove pretpostavke direktno sledi da je \( x \in \text{Cl}(A) \) i \( x \in \text{Cl}(X - A) \).
Kako važi identitet \( \text{Cl}(X - A) = X - \text{Int}(A) \), zaključujemo da tačka \( x \) ne pripada unutrašnjosti skupa \( A \).
Prema tome, važi \( x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A \), čime je pokazano da je \( x \) zaista tačka ruba skupa \( A \).