Topologija otvorenih skupova
Topologija T na skupu X je kolekcija podskupova koji se smatraju otvorenima. Takva kolekcija mora zadovoljiti dva osnovna pravila:
- Prazni skup Ø i cijeli skup X uvijek su otvoreni.
- Unija bilo kojeg broja otvorenih skupova mora biti otvorena, a presjek konačnog broja otvorenih skupova također mora biti otvoren.
Drugim riječima, topologija T sadrži samo one podskupove skupa X koji su proglašeni otvorenima, a uz to mora biti zatvorena na operacije unije i presjeka.
Kada spominjemo kolekciju skupova, govorimo o skupu čiji su elementi drugi skupovi ili njihovi podskupovi.
Skup X zajedno s topologijom T čini topološki prostor, koji se uobičajeno zapisuje kao uređeni par (X,T).
Napomena: Često se u govoru kaže da je X topološki prostor, no zapravo je nužno postojanje i skupa X i topologije T. Tek zajedno čine jedan topološki prostor.
Zašto je prazni skup uvijek otvoren?
To je konvencija u topologiji: prazni skup u svakom je topološkom prostoru otvoren. Ovo pravilo osigurava konzistentnost definicije i olakšava rad s otvorenim skupovima.
Primjer
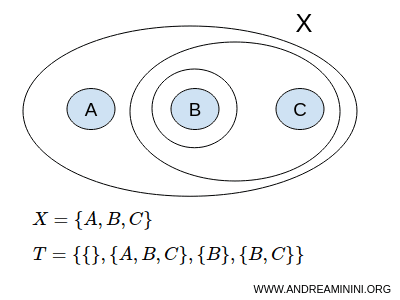
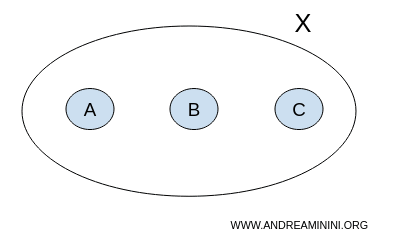
Razmotrimo skup X koji sadrži tri elementa A, B i C:
$$ X = \{ A,B,C \} $$
Jedna moguća topologija T može sadržavati podskupove { }, {A,B,C}, {B} i {B,C}:
$$ T = \{ \{ \},\{A,B,C\}, \{B\}, \{B,C\} \} $$
Prazni skup { } predstavlja Ø, dok {A,B,C} označava cijeli skup, odnosno nepravilne podskupove skupa X.
Po definiciji su i Ø i X uvijek otvoreni skupovi.
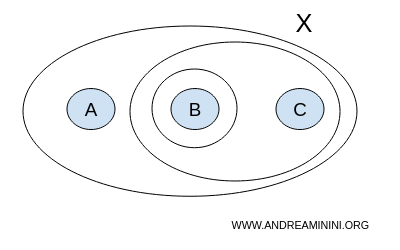
Kako bismo provjerili je li T doista topologija, trebamo vidjeti ostaje li T zatvorena na unije i presjeke svojih podskupova.
Primijetimo da je unija bilo kojih podskupova iz T ponovno element T:
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
Isto vrijedi i za presjeke:
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
Budući da su oba uvjeta ispunjena, T je doista topologija na X.
Drugi primjer
Pogledajmo sada sličnu situaciju s istim skupom X:
$$ X = \{ A,B,C \} $$
Ovaj put u kolekciju dodajemo podskup {A}:
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
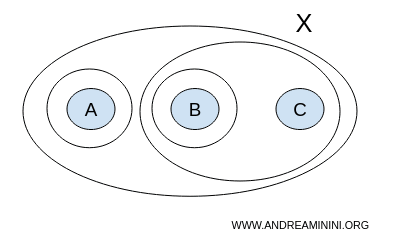
Na prvi pogled izgleda kao prihvatljiva topologija. Međutim, pojavljuje se problem. Unija {A} i {B} iznosi {A,B}, ali taj skup ne postoji u kolekciji T:
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T $$
To znači da T nije zatvorena na unije, pa ne može biti topologija. Iako su {A} i {B} u kolekciji označeni kao otvoreni skupovi, njihova unija to nije, jer nije uključena u T.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Zbog toga T ne može biti topologija na X. Ovo jasno pokazuje koliko je važno pravilo zatvorenosti na unije i presjeke.
Nakon ova dva primjera, ideja topologije postaje puno jasnija. Daljnje primjere moguće je razvijati na isti način, mijenjajući skup X ili kolekciju T te provjeravajući zadovoljava li potrebne uvjete.