Topološki podprostor

Topološki podprostor je podskup nekog topološkog prostora kojem pridružujemo posebnu topologiju izvedenu iz izvornog prostora. Ideja je jednostavna: u podprostoru zadržavamo onu strukturu otvorenih i zatvorenih skupova koju već ima veći prostor, samo prilagođenu novom okruženju.

Ako je \( (X, T) \) topološki prostor, pri čemu je \( X \) skup, a \( T \) kolekcija otvorenih skupova, tada za svaki podskup \( Y \subseteq X \) induciranu topologiju na \( Y \) definiramo kao: \[ T_Y = \{ U \cap Y \mid U \in T \} \]

Drugim riječima, skup \( V \subseteq Y \) bit će otvoren u \( Y \) samo ako se može dobiti kao presjek nekog otvorenog skupa iz \( X \) sa samim \( Y \). Time podprostor dobiva svoju vlastitu topologiju koja je potpuno usklađena s većom strukturom prostora \( X \).

Otvoreni skupovi u podprostoru uvijek imaju oblik \( U \cap Y \), gdje je \( U \) otvoren u \( X \). Isto vrijedi i za zatvorene skupove, samo što tada polazimo od zatvorenog skupa u \( X \).

Napomena: Skup koji je otvoren u podprostoru ne mora biti otvoren i u izvornom prostoru. Ponekad je otvoren u jednom, zatvoren u drugom, ili čak istovremeno otvoren i zatvoren u oba. Takvi se skupovi nazivaju klopen skupovi.

Primjer: podprostor u realnim brojevima

Uzmimo standardnu topologiju na \( \mathbb{R} \), u kojoj su osnovni otvoreni skupovi otvoreni intervali. Promotrimo podskup \( Y = [0, 1] \).

Inducirana topologija na \( Y \) sastoji se od svih skupova koje možemo dobiti kao presjek otvorenih intervala iz \( \mathbb{R} \) s intervalom \( [0, 1] \).

Na primjer, interval (-1, 0.5) je otvoren u \( \mathbb{R} \):

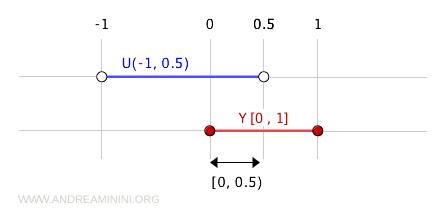
Njegov presjek s \( Y = [0, 1] \) daje otvoreni skup u induciranoj topologiji:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Zato je interval \( [0, 0.5) \) otvoren u \( Y \), iako nije otvoren u cijelom prostoru \( \mathbb{R} \).

S druge strane, skup \( [0, 0.5] \) zatvoren je u podprostoru jer nastaje presjecanjem zatvorenog intervala \( [-1, 0.5] \) s \( Y \):

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Vidimo da podprostor preuzima strukturu topologije iz \( X \). Otvoreni skupovi u \( Y \) nisu ništa drugo nego prilagođeni otvoreni skupovi iz većeg prostora.

Napomena: Intervali [0,a) ili (a,1], s \( 0 < a < 1 \), nisu otvoreni u \( \mathbb{R} \), ali jesu u \( Y = [0,1] \). Razlog je jednostavan: dobivaju se kao presjeci odgovarajućih otvorenih intervala u \( \mathbb{R} \) s \( Y \).

Poneki skupovi ostaju otvoreni i u \( X \) i u \( Y \), poput intervala \( (0.2, 0.8) \). Isto vrijedi i za zatvorene skupove, primjerice \( [0.2, 0.8] \).

Poseban je slučaj cijeli interval \( [0, 1] \) koji je istovremeno otvoren i zatvoren u induciranoj topologiji na \( Y \). Takvi skupovi nazivaju se klopen.

Primjer 2: Još jedan primjer: cijeli brojevi kao podprostor

Razmotrimo ponovno \( \mathbb{R} \) sa standardnom topologijom. U njoj je svaki otvoreni interval \( (a, b) \) otvoren.

Skup cijelih brojeva \( \mathbb{Z} \) čini podprostor \( \mathbb{R} \), jer se svaki pojedini cijeli broj može dobiti kao presjek odgovarajućeg otvorenog intervala s \( \mathbb{Z} \). Na primjer:

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

To vrijedi za svaki cijeli broj, pa je svaki singleton otvoren u induciranoj topologiji na \( \mathbb{Z} \).

Štoviše, svaki podskup od \( \mathbb{Z} \) bit će otvoren. Primjer:

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Inducirana topologija na \( \mathbb{Z} \) potpuno odgovara diskretnoj topologiji.

Napomena: Diskretna topologija na \( \mathbb{Z} \) nije podtopologija topologije na \( \mathbb{R} \), nego samostalna topologija. Ipak, inducirana topologija koju \( \mathbb{Z} \) nasljeđuje iz \( \mathbb{R} \) zapravo je ekvivalentna diskretnoj topologiji.

Primjer 3

Da bismo bolje razumjeli induciranu topologiju, pogledajmo jedan od najpoznatijih geometrijskih objekata: jediničnu sferu \( S^2 \) u trodimenzionalnom euklidskom prostoru \( \mathbb{R}^3 \). U ovom prostoru otvoreni skupovi nastaju kao unije otvorenih lopti, a sfera se definiše jednostavnom jednačinom:

$$ S^2 = \{ (x, y, z) \mid x^2 + y^2 + z^2 = 1 \} $$

Iako se nalazi „unutar” \( \mathbb{R}^3 \), sfera ima svoju sopstvenu topologiju. Ta topologija nastaje tako što uzmemo sve otvorene skupove iz \( \mathbb{R}^3 \) i presiječemo ih sa samom sferom. Ovo daje kolekciju otvorenih skupova na površini sfere, koju zovemo inducirana topologija:

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ otvoren u } \mathbb{R}^3 \} $$

Na taj način konstrukcija ostaje potpuno usklađena sa okolinom: ono što je lokalno otvoreno u \( \mathbb{R}^3 \), postaje otvoreno i u samoj sferi, samo ograničeno na njenu površinu.

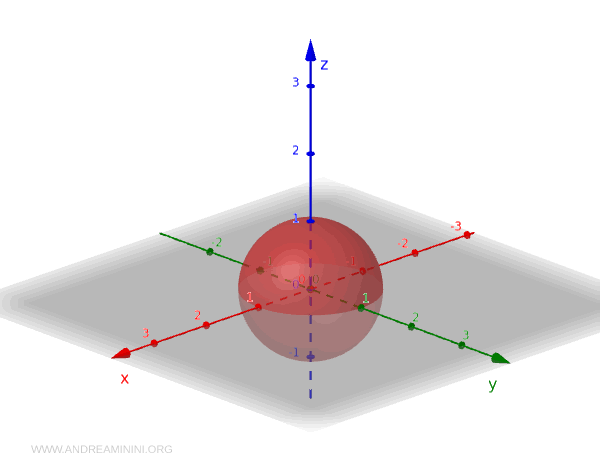
Evo nekoliko konkretnih primjera kako otvoreni skupovi izgledaju na sferi:

• Presjek sa skupom koji obuhvata cijelu sferu
  Zamislimo kuglu poluprečnika većeg od 1, na primjer: $$ U = \{ (x, y, z) \mid x^2 + y^2 + z^2 < 2 \} $$ Svaka tačka sfere ispunjava uslov \( 1 < 2 \), pa je: $$ U \cap S^2 = S^2 $$ Drugim riječima, u podprostornoj topologiji sfera je otvorena u samoj sebi.
• Otvoreni dio površine sfere
  Razmotrimo otvoreni poluprostor: $$ U = \{ (x, y, z) \mid z > 0 \} $$ Kada ga presiječemo sa sferom, dobijamo: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Ovaj skup predstavlja gornju hemisferu, tipičan primjer otvorenog područja na sfernoj površini.
• Osnovna topološka pravila na sferi
  
  • Prazan skup i cijela sfera uvijek su otvoreni.
  • Presjek konačno mnogo otvorenih skupova ostaje otvoren.
  • Proizvoljna unija otvorenih skupova, uključujući beskonačne unije, takođe ostaje otvorena.

Kao podprostor, sfera nasljeđuje sve bitne elemente topologije iz \( \mathbb{R}^3 \). Otvoreni skupovi na njenoj površini nastaju jednostavnom i intuitivnom operacijom: ograničavanjem otvorenih skupova okoline na samu sferu.

Svojstva inducirane topologije

Ista logika važi za svaki topološki podprostor. Osnovna svojstva inducirane topologije mogu se svesti na nekoliko ključnih pravila:

1. Otvoreni skupovi imaju oblik presjeka
   Svaki otvoreni skup u \( Y \) može se napisati kao \( U \cap Y \), gdje je \( U \) otvoren u prostoru \( X \).
2. Prazan skup i cijeli prostor uvijek su otvoreni
   To slijedi direktno iz definicije:
   - \( \emptyset = \emptyset \cap Y \)
   - \( Y = X \cap Y \)
3. Konačni presjeci ostaju otvoreni
   Ako su \( V_1, \ldots, V_n \) otvoreni u \( Y \), tada postoji kolekcija otvorenih skupova \( U_1, \ldots, U_n \) u \( X \) takva da: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap \cdots \cap U_n) \cap Y $$
4. Proizvoljne unije ostaju otvorene
   Čak i ako se radi o beskonačno mnogo skupova, unija otvorenih skupova u \( Y \) uvijek ostaje otvorena: $$ \bigcup_{\alpha \in I} V_\alpha = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$

Napomene

Inducirana topologija se pojavljuje u mnogo različitih konteksta. Posebno je važna u analizi geometrijskih struktura koje su „ugrađene” u veće prostore.

• Za svaki podskup \( Y \subseteq \mathbb{R}^n \) uobičajena topologija na \( Y \) savršeno se poklapa sa topologijom koju \( Y \) dobija kao podprostor \( \mathbb{R}^n \).

  Primjer: Neka je \( Y = [-1,0) \cup (0,1] \subseteq \mathbb{R} \). Ovi intervali su otvoreni u \( Y \) jer se dobijaju presjecanjem \( Y \) sa otvorenim intervalima iz \( \mathbb{R} \): $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Tako dobijena topologija identična je induciranoj topologiji. Istovremeno, svaki od ovih intervala zatvoren je u \( Y \) jer mu je komplement otvoren. Takvi skupovi nazivaju se klopen.

• Teorem o bazi u induciranoj topologiji
  Ako je \( B_X \) baza topologije na \( X \), tada presjeci oblika: $$ B \cap Y $$ gdje je \( B \in B_X \), čine bazu inducirane topologije na \( Y \). Ovo daje praktičan način da se topologija podprostora izgradi direktno iz baze nadređenog prostora.

Inducirana topologija se pojavljuje gotovo svuda gdje god analiziramo objekte koji žive unutar većih struktura, od geometrije do analize i diferencijalnih mnogostrukosti. Njena jednostavna definicija čini je jednim od najintuitivnijih pojmova u opštoj topologiji.