Standardna topologija na skupu ℝ

Standardna (ili uobičajena) topologija na skupu $ \mathbb{R} $ određuje se pomoću otvorenih intervala $ (a, b) $, gde važi $ a < b $, kao i svih njihovih konačnih ili beskonačnih unija. Takvi skupovi čine osnovu pojma otvorenih skupova u matematičkoj topologiji.

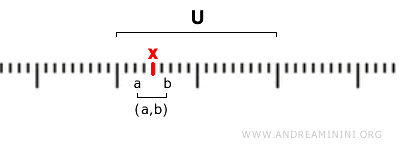
Formalno, skup $ U $ je otvoren ako za svaku tačku $ x \in U $ postoji otvoreni interval $ (a, b) $ takav da $ x \in (a, b) $ i $ (a, b) \subseteq U $.

$$ x \in (a,b) \subseteq U $$

Drugim rečima, svaka tačka otvorenog skupa nalazi se unutar nekog otvorenog intervala koji u potpunosti pripada tom skupu.

primjer otvorenog skupa

U okviru standardne topologije na realnoj pravoj, otvoreni skupovi imaju nekoliko ključnih svojstava:

Otvoreni intervali
Svi otvoreni skupovi mogu se predstaviti kao unije otvorenih intervala $ (a, b) $ za koje važi $ a < b $. Te unije mogu biti konačne ili beskonačne.
Osnovne operacije
U ovoj topologiji, dve operacije čuvaju otvorenost:
- Unija skupova: Svaka, pa i beskonačna, unija otvorenih skupova je otvoren skup.
- Konačni presek: Presek konačnog broja otvorenih skupova takođe je otvoren skup.

Standardna topologija je najčešće korišćeni tip topologije na $ \mathbb{R} $. Njena važnost potiče iz činjenice da na prirodan način opisuje pojmove kao što su blizina, otvorenost i kontinuitet, koji su temelj matematičke analize.

Napomena: Na $ \mathbb{R} $ i drugim skupovima mogu se definisati i druge vrste topologija, zasnovane na različitim bazama. Takve varijante koriste se za proučavanje specifičnih svojstava prostora ili za sagledavanje matematičkih struktura iz drugačije perspektive.

Primjer iz prakse

Baza standardne topologije na $ \mathbb{R} $ sastoji se od svih otvorenih intervala $ (a, b) $ gde $ a < b $.

$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$

Osnovno svojstvo ove topologije jeste da za svaku tačku $ x $ iz otvorenog skupa $ U $ uvek postoji otvoreni interval centriran u $ x $ koji se u potpunosti nalazi unutar $ U $. Time se precizno ispunjava definicija otvorenog skupa.

$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$

Drugim rečima, $ U $ je otvoren skup u standardnoj topologiji na $ \mathbb{R} $. Upravo se ova topologija koristi kada formalno definišemo pojmove kontinuiteta, granice i konvergencije u analizi.

Primjer 2

Razmotrimo interval $ (0,1) $, koji ne uključuje krajnje tačke $ 0 $ i $ 1 $. Posmatrajmo njegovu topološku strukturu u okviru standardne topologije.

slučaj intervala (0,1)

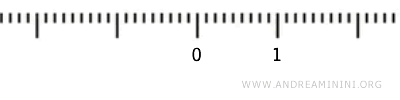
U indukovanoj topologiji, podskup $ U \subset (0, 1) $ je otvoren ako za svaku tačku $ x \in U $ postoji otvoreni interval $ (a, b) $ u $ \mathbb{R} $ takav da $ x \in (a, b) $ i $ (a, b) \cap (0,1) \subseteq U $.

Interval $ (0,1) $ može se prikazati kao presek više otvorenih skupova u standardnoj topologiji na $ \mathbb{R} $, pa tako poseduje dobro definisanu topološku strukturu.

Prema tome, interval $ (0,1) $ je topološki prostor sa topologijom indukovanom iz standardne topologije na $ \mathbb{R} $.

Na primer, intervali $ (0.1, 0.5) $, $ (0.2, 0.9) $ i njihova unija $ (0.1, 0.5) \cup (0.6, 0.8) $ su otvoreni skupovi u $ (0,1) $ prema indukovanoj topologiji. Drugim rečima, otvoreni skupovi u $ (0,1) $ su upravo oni otvoreni skupovi u $ \mathbb{R} $ čiji presek sa $ (0,1) $ ostaje u potpunosti unutar tog intervala.

Kako je $ (0,1) $ podprostor topološkog prostora $ \mathbb{R} $, on nasleđuje njegova osnovna svojstva, uključujući pojmove otvorenosti, zatvorenosti i kontinuiteta funkcija.

Primjer 3

Razmotrimo konačan skup $ X = \{1,2,3\} $, koji se sastoji od tri prirodna broja. Postavlja se pitanje može li ovaj skup imati topološku strukturu izvedenu iz standardne topologije na $ \mathbb{R} $.

U ovom slučaju, pojedinačni elementi skupa $ X $ ne mogu biti otvoreni, jer se baza standardne topologije sastoji od otvorenih intervala, a oni ne odgovaraju diskretnom skupu kao što je $ X $.

Na primer, ako posmatramo element $ \{2\} $ iz $ X $, možemo ga smestiti u otvoreni interval $ (2-\epsilon, 2+\epsilon) $, ali taj interval sadrži beskonačno mnogo realnih brojeva koji ne pripadaju $ X $. Dakle, $ \{2\} $ se ne može smatrati otvorenim skupom u standardnoj topologiji na $ \mathbb{R} $.
primjer sa brojem 2

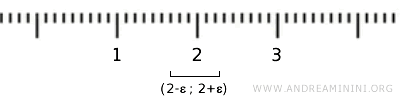
Ako posmatramo $ X $ kao podskup realnih brojeva, indukovana topologija (topologija podprostora) na $ X $ sadrži samo dva otvorena skupa: prazan skup i sam skup $ X $. Takva struktura je trivijalna sa topološkog stanovišta.

Da bi se konačnom skupu poput $ X $ dodelila bogatija topološka struktura, koristi se diskretna topologija, u kojoj su svi podskupovi od $ X $ po definiciji otvoreni.

Na taj način topologija omogućava da se različiti tipovi prostora posmatraju i analiziraju kroz jedinstveni formalni okvir koji povezuje intuiciju i apstrakciju.