Unutrašnjost skupa
U topologiji, pojam unutrašnjosti skupa igra ključnu ulogu u razumijevanju strukture prostora. Za skup \( A \) u topološkom prostoru \( X \), unutrašnjost je definisana kao unija svih otvorenih podskupova koji se nalaze unutar \( A \). Ova vrijednost najčešće se označava sa \( \text{Int}(A) \) ili \( A^\circ \).
Praktično, unutrašnjost predstavlja najveći otvoreni skup koji se u potpunosti nalazi u posmatranom skupu \( A \).
Nijedan drugi otvoreni skup sadržan u \( A \) ne može biti veći od njegove unutrašnjosti, što ovom pojmu daje posebno jasno i precizno značenje.
Napomena : Pošto je definisana kao unija otvorenih skupova, unutrašnjost skupa uvijek je otvorena.
Formalna definicija kaže da unutrašnjost \( A \) čine sve tačke u \( A \) koje imaju neko otvoreno susjedstvo potpuno smješteno unutar \( A \).
$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ je otvoren skup u } X \} $$
Drugim riječima, tačka \( x \) nalazi se u unutrašnjosti skupa ako postoji otvoreni skup \( U \) koji sadrži \( x \) i ne izlazi iz \( A \).
Važno je zapamtiti da unutrašnjost ne zavisi samo od skupa \( A \), nego prije svega od topologije prostora \( X \). Promijenimo li topologiju, mijenja se i pojam unutrašnjosti.
Primjer iz standardne topologije
Uzmimo interval \( A = [0,1] \) u skupu realnih brojeva \( \mathbb{R} \) sa standardnom topologijom. U njemu se nalaze svi brojevi između 0 i 1, uključujući krajnje tačke.
Unutrašnjost ovog intervala je otvoreni interval \( (0,1) \):
$$ \text{Int}(A) = (0,1) $$
Krajnje tačke 0 i 1 ne pripadaju nijednom otvorenom intervalu koji bi ostao u potpunosti unutar \( [0,1] \), pa zato nisu dio unutrašnjosti.
Primjer 2
Posmatrajmo sada skup \( A = [0,1) \) u istoj topologiji. Iako se struktura intervala mijenja samo na jednoj granici, njegova unutrašnjost ostaje ista:
\[ \text{Int}(A) = (0,1) \]
Najveći otvoreni skup unutar \( A \) i dalje je otvoreni interval bez krajnjih tačaka, a tačka 0 i ovdje nije dio nijednog otvorenog intervala koji bi ostao u potpunosti unutar \( [0,1) \).
Napomena : U standardnoj topologiji na \( \mathbb{R} \), otvoreni skupovi uvijek se mogu predstaviti kao unije otvorenih intervala. To je razlog zašto tačka 0 ostaje izvan unutrašnjosti u oba primjera.
Primjer iz diskretne topologije
Sada razmotrimo isti interval \( A = [0,1) \), ali u topologiji gdje su svi podskupovi otvoreni - diskretnoj topologiji.
U ovom okruženju, svaka tačka ima otvoreno susjedstvo sadržano u \( A \), jer je svaki podskup po definiciji otvoren.
U diskretnoj topologiji svaki podskup je otvoren: intervali, konačni skupovi, proizvoljne unije i sam skup \( [0,1) \).
Zbog toga je:
$$ \text{Int}(A) = A = [0,1) $$
U diskretnoj topologiji unutrašnjost svakog skupa jednaka je tom skupu, bez izuzetka.
Napomena : Ovo jasno pokazuje koliko izbor topologije utiče na geometriju i intuitivni pojam susjedstva, a time i na samu definiciju unutrašnjosti.
Primjer sa konačnim prostorom
Razmotrimo sada topološki prostor \( X = \{a, b, c\} \) sa diskretnom topologijom. U takvom prostoru svaki podskup je otvoren:
- Prazni skup i cijeli prostor su otvoreni.
- Svaka pojedinačna tačka čini otvoren skup.
- Podskupovi sa dvije tačke takođe su otvoreni.
Posmatrajmo skup \( A = \{b, c\} \). Unutrašnjost se dobija tako što uzmemo uniju svih otvorenih podskupova sadržanih u \( A \):
\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]
U skladu sa svojstvima diskretne topologije, dobijamo da je unutrašnjost upravo sam skup \( A \).
Napomena : Ovo pravilo važi za svaki podskup u diskretnoj topologiji. Ako su svi skupovi otvoreni, onda je unutrašnjost uvijek jednaka početnom skupu.
Teorem o unutrašnjosti skupa
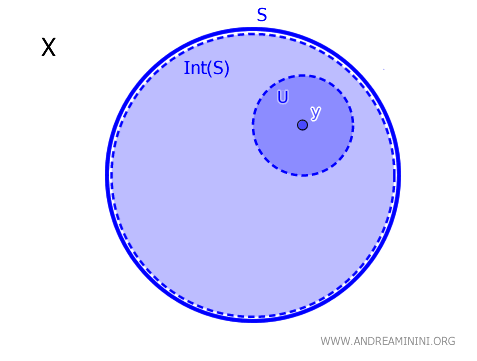
U topološkom prostoru \( X \), za podskup \( S \subseteq X \) i tačku \( y \in X \), kažemo da \( y \) pripada unutrašnjosti skupa \( S \), označeno \( \operatorname{Int}(S) \), ako i samo ako postoji otvoreni skup \( U \) takav da \( y \in U \subseteq S \). Formalno: $$ y \in \text{Int}(S) \iff \exists \ U \text{ otvoren, sa } y \in U \subseteq S $$
Drugim riječima, tačka \( y \) je unutrašnja tačka skupa \( S \) upravo kada posjeduje otvoreno susjedstvo u potpunosti sadržano u \( S \). Ovo je jedan od najosnovnijih i najčešće korištenih kriterija u općoj topologiji.
Teorem precizno opisuje kada se tačka može smatrati unutrašnjom, povezujući lokalnu strukturu oko tačke s globalnom strukturom skupa.
Dokaz
- Neophodan uslov: Ako \( y \in \operatorname{Int}(S) \), postoji otvoreni skup \( U \subseteq X \) za koji vrijedi \( y \in U \subseteq S \). Ovo je direktna posljedica definicije unutrašnjosti.
- Dovoljan uslov: Ako postoji otvoreni skup \( U \) s osobinom \( y \in U \subseteq S \), tada je \( y \) unutrašnja tačka skupa \( S \), jer se unutrašnjost definiše upravo kao unija svih otvorenih skupova sadržanih u \( S \).
Napomena: Teorem daje jednu od najvažnijih karakterizacija unutrašnjosti. Povezuje otvorene skupove, lokalnu strukturu susjedstava i globalna topološka svojstva skupa.
Primjer
Razmotrimo skup \( A = [1,3] \), zatvoreni interval u \( \mathbb{R} \) opremljen standardnom topologijom.
$$ A = [1,3] $$
Interval obuhvata sve realne brojeve između 1 i 3, uključujući krajnje tačke.
Određivanje unutrašnjosti skupa \( A \)
Da bismo odredili \( \operatorname{Int}(A) \), tražimo otvoreni skup \( U \) sadržan u \( A \) čije tačke su unutrašnje tačke.
- Izbor otvorenog skupa
Prirodan izbor je otvoreni interval \( U = (1,3) \), koji je uobičajeni primjer otvorenog skupa u standardnoj topologiji na \( \mathbb{R} \). - Provjera uključenosti
Sve tačke iz \( (1,3) \) nalaze se u zatvorenom intervalu \( [1,3] \). Tačke 1 i 3 ne pripadaju \( U \), što je u skladu s njegovom definicijom.
Otvoreni interval \( (1,3) \) je najveći otvoreni podskup skupa \( A \), pa vrijedi: $$ \operatorname{Int}(A) = (1,3) $$
Napomena: Tačke 1 i 3 nisu unutrašnje, jer nijedan otvoreni interval ne može obuhvatiti te tačke a da ostane u potpunosti unutar \( [1,3] \). Ovo je tipičan primjer razlike između granica i unutrašnjih tačaka.
Svojstva unutrašnjosti
U nastavku slijede temeljna i u standardnoj literaturi široko korištena svojstva unutrašnjosti. Ona opisuju kako unutrašnjost reaguje na osnovne operacije nad skupovima.
- Unija unutrašnjosti
Uvijek vrijedi: $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ Ova inkluzija može biti stroga, što naglašava da operacija unutrašnjosti ne „distribuira“ u potpunosti preko unije. - Presjek unutrašnjosti
Za presjek vrijedi perfektna jednakost: $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$ Ovo svojstvo pokazuje da operacija unutrašnjosti komutira s presjekom. - Unutrašnjost komplementa i komplement adherencije
Jedan od ključnih odnosa u topologiji glasi: $$ \text{Int}(X - A) = X - \text{Cl}(A) $$ gdje \( \text{Cl}(A) \) označava adherenciju (zatvaranje) skupa \( A \). - Adherencija komplementa i komplement unutrašnjosti
Takođe vrijedi: $$ \text{Cl}(X - A) = X - \text{Int}(A) $$ Ovaj odnos je dual prethodnom i ilustruje simetriju između operacija unutrašnjosti i zatvaranja.
Napomene
Slijede neke dodatne činjenice koje često igraju važnu ulogu u analizi topoloških svojstava:
- Ako je \( U \) otvoren i \( U \subseteq A \), tada je \( U \subseteq \operatorname{Int}(A) \)
To proizlazi iz činjenice da je unutrašnjost najveći otvoreni podskup skupa \( A \). - Ako je \( A \subseteq B \), tada \( \operatorname{Int}(A) \subseteq \operatorname{Int}(B) \)
Unutrašnjost je monotona operacija i čuva uključenost skupova. - Skup je otvoren ako i samo ako je jednak svojoj unutrašnjosti
Ovo je klasična i fundamentalna karakterizacija otvorenih skupova. - Računanje unutrašnjosti u jeziku R
Okruženje R omogućava praktične topološke operacije nad skupovima, što uključuje i određivanje njihovih unutrašnjosti u numeričkim i vizuelnim analizama.