Unutrašnjost unije dvaju skupova
U topologiji se često susreće pitanje kako se ponaša unutrašnjost kada kombinujemo različite skupove. Ključno svojstvo glasi: za bilo koja dva skupa \( A \) i \( B \), unija njihovih unutrašnjosti uvijek je sadržana u unutrašnjosti njihove unije: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Ovo uključivanje je općenito tačno, ali ne mora biti jednakost.
Drugim riječima, unutrašnjost unije nikada ne može biti manja od unije unutrašnjosti. Ipak, dva izraza se ne moraju poklapati. U mnogim slučajevima razlika između njih je vrlo značajna, posebno kada se skupovi dodiruju samo na granici.
Jednakost: $$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$ vrijedi samo u specifičnim konfiguracijama. Čim se javi komplikacija na granicama, uključivanje postaje strogo:
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Primjer: otvoreni intervali
Počnimo s jednostavnom situacijom u skupu realnih brojeva \(\mathbb{R}\). Uzmimo dva otvorena intervala:
$$ A = (0, 2), \quad B = (1, 3) $$
Unutrašnjost svakog otvorenog intervala jednaka je njemu samom, pa je:
$$ \text{Int}(A) = (0, 2), \quad \text{Int}(B) = (1, 3) $$
Njihova unija daje:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 3) $$
Budući da je i unija samih intervala:
$$ A \cup B = (0, 3) $$
dobijamo:
$$ \text{Int}(A \cup B) = (0, 3) $$
U ovom primjeru dvije strane su jednake. Takve situacije se javljaju kada se otvoreni skupovi preklapaju tako da njihova unija ostaje otvorena i povezana.
Primjer: zatvoreni intervali
Sada posmatrajmo drugačiji slučaj:
$$ A = [0, 2], \quad B = [2, 3] $$
Njihove unutrašnjosti su:
$$ \text{Int}(A) = (0, 2), \quad \text{Int}(B) = (2, 3) $$
Unija daje zatvoreni interval:
$$ A \cup B = [0, 3] $$
a njegova unutrašnjost je:
$$ \text{Int}(A \cup B) = (0, 3) $$
Uključivanje:
$$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$
ostaje tačno, ali jednakost ne vrijedi. Razlog je jednostavan: tačka \( 2 \) pripada unutrašnjosti unije, ali ne pripada nijednoj od unutrašnjosti pojedinačnih intervala. Ovaj primjer jasno pokazuje da granične tačke mogu stvoriti razliku između dvije strane izraza.
Primjer: disjunktni otvoreni intervali
Uzmimo još jednostavniju konfiguraciju:
$$ A = (0, 1), \quad B = (2, 3) $$
Unutrašnjosti su nepromijenjene, a i unija je otvorena:
$$ \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$
Ovdje se jednakost ponovno ostvaruje. Ključ je u tome što se otvoreni intervali ne dodiruju, pa ne nastaje nova unutrašnjost koja bi ih povezivala.
Primjer iz ravnine: preklapajući diskovi
Razmotrimo sada primjer u \(\mathbb{R}^2\). Dva otvorena diska djelomično se preklapaju:
$$ A = \{ (x, y) : x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) : (x - 0{,}5)^2 + y^2 < 1 \} $$
Kako su oba skupa otvorena, njihove unutrašnjosti su isti skupovi. Unija je jednostavno spojena oblast koja sadrži oba diska:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
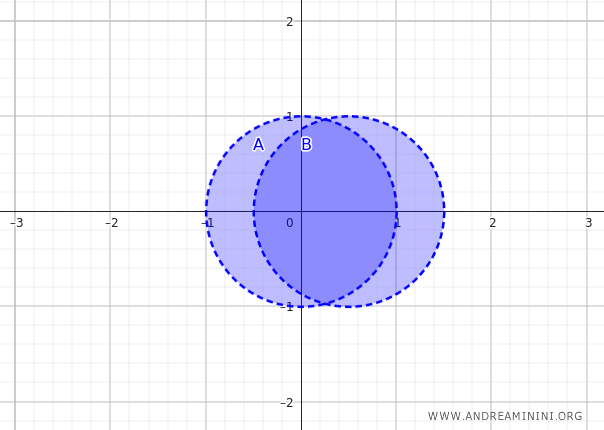
Unutrašnjost njihove unije ostaje ista, jer su oba diska otvorena i njihova unija nema novih graničnih tačaka koje bi mijenjale unutrašnjost:
$$ \text{Int}(A \cup B) = A \cup B $$
Zašto ovo svojstvo vrijedi
Da bismo razumjeli zašto se uvijek dobija uključivanje:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
podsjetimo se definicije unutrašnjosti. Tačka je u unutrašnjosti skupa \( X \) ako postoji otvoreni skup koji sadrži tu tačku i u potpunosti je sadržan u \( X \).
Uz to, svaki otvoreni skup unutar \( A \) ili \( B \) ostaje otvoreni skup i unutar njihove unije. To znači da svaka tačka koja ima dovoljno prostora da bude unutrašnja u jednom od skupova automatski ima prostora da bude unutrašnja i u njihovoj uniji.
Time zaključujemo da je uključivanje uvijek tačno, iako jednakost zavisi od konkretne konfiguracije skupova.
Ovo svojstvo ima važnu ulogu u topologiji jer pokazuje kako se lokalna struktura skupova ponaša kada ih kombinujemo. Razlika između striktne i nestriktne situacije često otkriva fine detalje njihove geometrije i načina na koji se njihovi rubovi dodiruju ili preklapaju.