Diskretna topologija
Diskretna topologija \( T \) je najdetaljnija topologija koja se može definisati na skupu \( X \), jer obuhvata sve njegove podskupove bez izuzetka.
U ovoj topologiji, svaki podskup skupa \( X \) smatra se otvorenim skupom. Drugim rečima, svi delovi skupa su otvoreni, što znači da je svaka tačka potpuno izolovana od drugih.
Odsustvo bilo kakvog pojma „bliskosti" čini diskretnu topologiju jedinstvenom: elementi su potpuno nezavisni, a svaka konfiguracija prostora je moguća.
Napomena. Topologija na skupu \( X \) je kolekcija podskupova (tzv. otvorenih skupova) koji zadovoljavaju tri osnovna pravila:
- Prazan skup i ceo skup \( X \) pripadaju kolekciji \( T \).
- Svaka proizvoljna unija elemenata iz \( T \) pripada \( T \).
- Svaki konačni presek elemenata iz \( T \) pripada \( T \).
Ova topologija se naziva „diskretna" jer tretira svaku tačku kao odvojenu i nezavisnu, bez pojma kontinuiteta ili susedstva.
Diskretna topologija je najbogatija moguća topologija, jer nijedna druga ne može sadržati veći broj otvorenih skupova. Ona ih obuhvata sve.
Napomena. Ova pravila predstavljaju osnovu topologije. Omogućavaju nam da precizno opišemo kako se elementi prostora mogu posmatrati kao „bliski" ili kontinuirani, što je ključno za razumevanje pojma kontinuiteta.
Osnovno svojstvo diskretne topologije
U diskretnoj topologiji svaki podskup topološkog prostora je istovremeno otvoren i zatvoren.
Razlog je jednostavan: ako su svi podskupovi otvoreni, njihovi komplementi su takođe otvoreni, pa su samim tim i zatvoreni.
U topologiji, skup se smatra zatvorenim ako je njegov komplement otvoren.
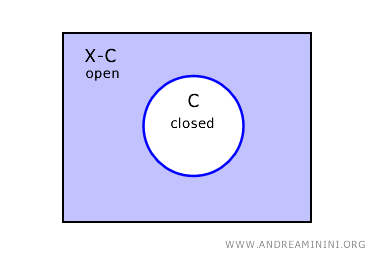
To znači da je u diskretnoj topologiji svaki podskup i otvoren i zatvoren, tj. klopen skup. Ovo važi za sve podskupove, ne samo za pojedinačne tačke.
Napomena. Pošto je komplement svakog podskupa takođe podskup skupa \( X \), a time i otvoren, sledi da je svaki podskup istovremeno i zatvoren. Drugim rečima, svi delovi prostora imaju isti „status" u pogledu otvorenosti i zatvorenosti.
Primer
Da bismo razumeli kako funkcioniše diskretna topologija, posmatrajmo jednostavan primer. Neka je skup \( X \) sastavljen od tri elementa:
$$ X = \{a, b, c\} $$
Svi mogući podskupovi ovog skupa su:
- Prazan skup: \(\emptyset\)
- Jednočlani skupovi: \(\{a\}\), \(\{b\}\), \(\{c\}\)
- Dvočlani skupovi: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
- Celokupan skup: \(\{a, b, c\}\)
U diskretnoj topologiji svi ovi podskupovi su otvoreni. Dakle, topologija \( T \) na skupu \( X \) glasi:
$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$
Ova kolekcija ispunjava sve uslove topologije: sadrži prazan skup i ceo skup, zatvorena je na proizvoljne unije i konačne preseke. Pošto su svi podskupovi otvoreni, diskretna topologija ne postavlja nikakva ograničenja u pogledu kontinuiteta.
Na primer, podskup \( \{a\} \) je otvoren po definiciji. Njegov komplement \( X \setminus \{a\} = \{b, c\} \) je takođe otvoren, pa je \( \{a\} \) i zatvoren.
Zaključujemo da je u diskretnoj topologiji svaki podskup istovremeno otvoren i zatvoren. Ovo važi za sve podskupove, bez izuzetka.