Separacija podskupa otvorenim skupovima

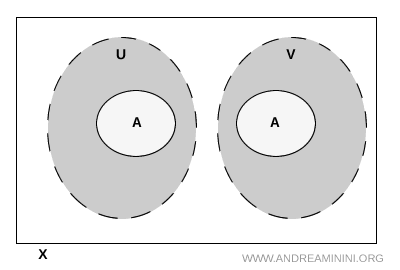
Kada proučavamo topološke prostore, jedno od osnovnih pitanja je kako prepoznati da je podskup razdvojen na dva jasno odvojena dijela. Najjednostavniji način da to provjerimo jeste pomoću otvorenih skupova istog prostora. Neka su $ U $ i $ V $ dva takva otvorena skupa. Oni razdvajaju podskup $ A $ ako su ispunjena tri precizno definirana uslova:

Njihova unija obuhvata cijeli skup $ A $ \[ A \subseteq U \cup V \]
Svaki od njih sadrži bar jednu tačku iz $ A $ \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
Ni jedna tačka iz $ A $ ne pripada istovremeno i $ U $ i $ V $ \[ U \cap V \cap A = \varnothing \]

Ako su ovi uslovi zadovoljeni, podskup $ A $ je stvarno podijeljen na dvije nezavisne cjeline. Jedna se nalazi u $ U $, druga u $ V $, a nijedna se ne preklapa s drugom. Upravo ta odsutnost zajedničkih tačaka unutar samog skupa $ A $ čini suštinu pojma separacije.

Ovakav pristup je standardan u topologiji i veoma pogodan za učenje, jer omogućava intuitivno razumijevanje apstraktnih definicija preko otvorenih skupova.

dijagram koji prikazuje separaciju podskupa otvorenim skupovima

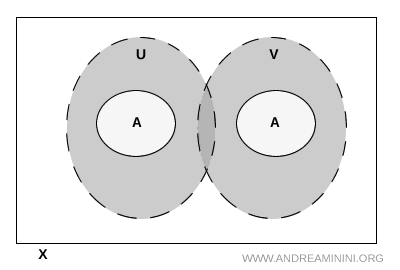
Napomena. Čak i ako se $ U $ i $ V $ međusobno sijeku izvan skupa $ A $, separacija ostaje važeća. Važno je isključivo to da njihov presjek ne sadrži nijednu tačku iz $ A $. To je jedini uslov koji se provjerava.

dijagram koji pokazuje da se otvoreni skupovi mogu sjeći izvan A bez narušavanja separacije

Primjer na realnoj pravoj

Da bismo vidjeli kako ova definicija funkcioniše u praksi, razmotrimo prostor $ X = \mathbb{R} $ i podskup:

$$ A = [-2,-1] \cup [1,2] $$

Ovdje imamo dva zatvorena intervala koji su jasno odvojeni.

Odaberimo sljedeće otvorene skupove:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Na realnoj pravoj situacija izgleda ovako:

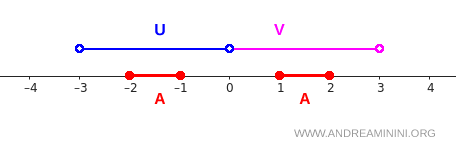
realna prava koja prikazuje otvorene skupove U i V te dvije komponente skupa A

Interval $ [-2,-1] $ nalazi se u $ U $, dok je $ [1,2] $ u $ V $. Uslovi separacije sada se mogu provjeriti veoma jednostavno:

1. Podskup $ A $ je u potpunosti sadržan u uniji skupova $ U $ i $ V $:

$$ A \subseteq U \cup V $$

2. Oba otvorena skupa sadrže dio skupa $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

3. Nijedna tačka iz $ A $ ne pripada istovremeno oba otvorena skupa:

$$ U \cap V \cap A = \varnothing $$

Ovaj primjer pokazuje kako dva otvorena intervala lako mogu razdvojiti skup sastavljen od dvije udaljene komponente. Primjer je jednostavan, ali vrlo ilustrativan za razumijevanje pojma separacije u topologiji.