Svaki povezani podskup sadržan je u jednoj povezanoj komponenti prostora

Neka su $ A $ i $ B $ dva podskupa topološkoga prostora $ X $. Pretpostavimo da je $ A $ povezan i da vrijedi $ A \subset B $. Ako se skup $ B $ može razdvojiti na dva disjunktna podskupa $ B_1 $ i $ B_2 $ u prostoru $ X $, tada se povezani podskup $ A $ ne može raspodijeliti između njih. Nužno vrijedi: $$ A \subset B_1 \quad \text{ili} \quad A \subset B_2 $$

Drugim riječima, povezani podskup ne može imati neprazan presjek s oba dijela jedne separacije.

Čim se povezani podskup nađe unutar skupa koji je razložen na dva disjunktna dijela, on mora u cijelosti pripadati samo jednom od njih. To je jedno od temeljnih obilježja pojma povezanosti u topologiji.

povezani podskup potpuno sadržan u jednom dijelu topološke separacije prostora

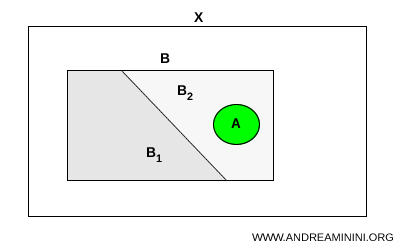
Intuitivno, povezani podskup možemo zamisliti kao neprekinuto uže smješteno u omotnicu. Ako se omotnica podijeli na dva odvojena pretinca, dok uže ostaje cijelo, ono se može nalaziti samo u jednom od njih. Da bi zauzelo oba, moralo bi se prekinuti. Upravo tu nemogućnost formalizira pojam povezanosti.

Konkretan primjer
Dokaz

Konkretan primjer

Razmotrimo topološki prostor

$$ X = \mathbb{R} $$

i njegov podskup

$$ B = (-3,4) $$

Skup $ B $ ima prirodnu separaciju na dva disjunktna podskupa:

$$ B_1 = (-3,0) $$

$$ B_2 = (0,4) $$

Vrijedi:

$$ B_1 \cap B_2 = \varnothing, \qquad B_1 \cup B_2 = B $$

Osim toga, oba su skupa $ B_1 $ i $ B_2 $ otvorena u topologiji podprostora induciranoj na $ B $. Zato oni doista čine separaciju skupa $ B $ u prostoru $ X $.

Sada uzmimo povezani podskup:

$$ A = (1,2) $$

Jasno je da vrijedi $ A \subset B_2 $. Podskup $ A $ u potpunosti je sadržan u jednom dijelu separacije, u skladu s općim pravilom.

Napomena. Ako bismo uzeli $ A = (-1,1) $, dobili bismo $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Takva situacija nije moguća. Budući da su $ B_1 $ i $ B_2 $ dijelovi separacije skupa $ B $, nijedan povezani podskup ne može biti raspodijeljen između njih. Kad bi to bilo moguće, i sam bi skup $ A $ imao separaciju, što je u suprotnosti s činjenicom da je interval $ (-1,1) $ povezan.

Dokaz

Pretpostavke

Neka su $ A $ i $ B $ podskupovi topološkoga prostora $ X $, pri čemu vrijedi

$$ A \subset X, \qquad B \subset X $$

Pretpostavimo:

$ A $ je povezan
$ A \subset B $
$ B_1 $ i $ B_2 $ čine separaciju skupa $ B $ u prostoru $ X $

Tvrdnja

Pod navedenim pretpostavkama vrijedi:

$$ A \subset B_1 \quad \text{ili} \quad A \subset B_2 $$

Dokaz

Budući da $ B_1 $ i $ B_2 $ čine separaciju skupa $ B $, vrijedi:

$ B_1 \cap B_2 = \varnothing $
$ B = B_1 \cup B_2 $
$ B_1 $ i $ B_2 $ otvoreni su u topologiji podprostora na $ B $

Pretpostavimo suprotno, da $ A $ nije u potpunosti sadržan ni u $ B_1 $ ni u $ B_2 $. Tada vrijedi:

$$ A \cap B_1 \neq \varnothing \qquad \text{i} \qquad A \cap B_2 \neq \varnothing $$

Kako je $ A \subset B $, imamo:

$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$

Skupovi $ A \cap B_1 $ i $ A \cap B_2 $ su disjunktni, neprazni i otvoreni u topologiji podprostora na $ A $.

Time oni definiraju separaciju skupa $ A $, što je u proturječju s pretpostavkom da je $ A $ povezan.

Iz toga slijedi da je početna pretpostavka pogrešna, pa nužno vrijedi:

$$ A \subset B_1 \quad \text{ili} \quad A \subset B_2 $$

Tvrdnja je time dokazana.

I tako dalje.